题目内容
设函数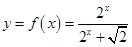 上两点
上两点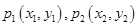 ,若
,若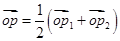 ,且P点的横坐标为
,且P点的横坐标为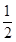 .
.
(Ⅰ)求P点的纵坐标;
(Ⅱ)若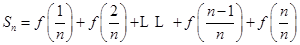 求
求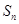 ;
;
(Ⅲ)记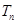 为数列
为数列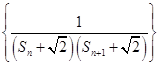 的前n项和,若
的前n项和,若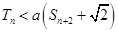 对一切
对一切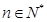 都成立,试求a的取值范围.
都成立,试求a的取值范围.
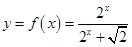 上两点
上两点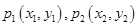 ,若
,若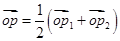 ,且P点的横坐标为
,且P点的横坐标为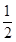 .
.(Ⅰ)求P点的纵坐标;
(Ⅱ)若
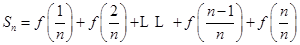 求
求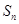 ;
;(Ⅲ)记
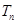 为数列
为数列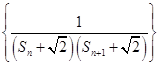 的前n项和,若
的前n项和,若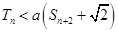 对一切
对一切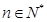 都成立,试求a的取值范围.
都成立,试求a的取值范围. (Ⅰ)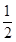 ;(Ⅱ)
;(Ⅱ)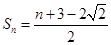 ;(Ⅲ)
;(Ⅲ)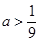 .
.
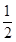 ;(Ⅱ)
;(Ⅱ)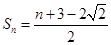 ;(Ⅲ)
;(Ⅲ)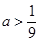 .
.试题分析:(Ⅰ)求
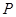 点的纵坐标,由于
点的纵坐标,由于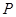 点满足
点满足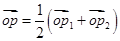 ,由向量加法的几何意义可知,
,由向量加法的几何意义可知,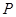 是
是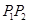 的中点,则
的中点,则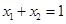 ,而
,而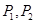 两点在函数
两点在函数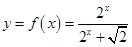 上,故
上,故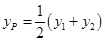 ,而
,而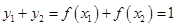 ,从而可得
,从而可得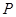 点的纵坐标;(Ⅱ)根据
点的纵坐标;(Ⅱ)根据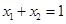 ,
,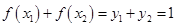 ,
,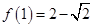 ,可利用倒序相加法求和的方法,从而可求的
,可利用倒序相加法求和的方法,从而可求的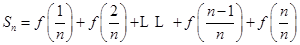 的值;(Ⅲ)记
的值;(Ⅲ)记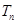 为数列
为数列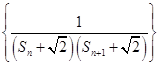 的前n项和,若
的前n项和,若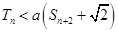 对一切
对一切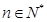 都成立,试求
都成立,试求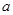 的取值范围,由(Ⅱ)可知
的取值范围,由(Ⅱ)可知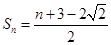 ,从而
,从而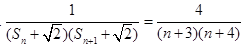 ,可用拆项相消法求和,若
,可用拆项相消法求和,若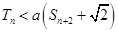 对一切
对一切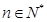 都成立,即
都成立,即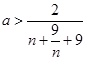 ,只需求出
,只需求出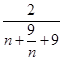 的最大值,从而得
的最大值,从而得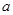 的取值范围.
的取值范围.试题解析:(Ⅰ)∵
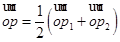 ,∴
,∴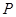 是
是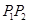 的中点,则
的中点,则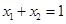 ------(2分)
------(2分)∴
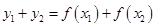
 .∴
.∴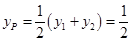 ,所以
,所以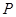 点的纵坐标为
点的纵坐标为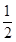 . (4分)
. (4分)(Ⅱ)由(Ⅰ)知
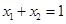 ,
,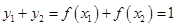 ,
,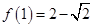 ,
,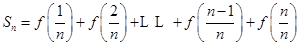 ,
,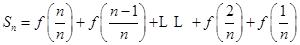 ,
,两式相加得
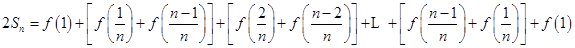
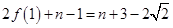 ∴
∴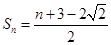 ; (8分)
; (8分)(Ⅲ)
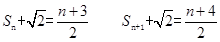
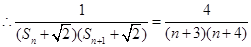

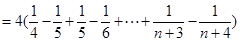
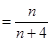 10分
10分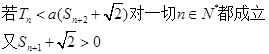
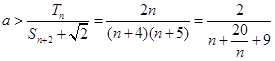 12分
12分
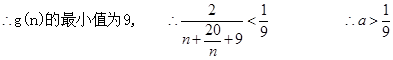 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
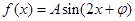
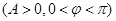 ,当
,当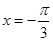 时取得最小值-4.
时取得最小值-4.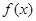 的解析式;
的解析式;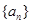 前n项和为
前n项和为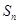 ,且
,且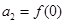 ,
,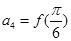 ,求数列
,求数列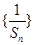 的前n项和
的前n项和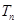 .
.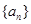 的前
的前 项和为
项和为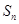 ,且
,且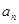 是
是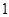 的等差中项,等差数列
的等差中项,等差数列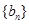 满足
满足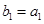 ,
, .
.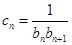 ,数列
,数列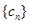 的前
的前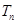 ,求
,求 的取值范围.
的取值范围.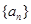 的前
的前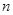 项和为
项和为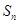 ,且
,且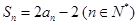 ,数列
,数列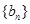 满足
满足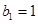 ,且
,且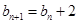 .
. 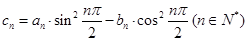 ,求数列
,求数列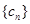 的前
的前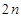 项和
项和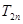 .
.  中,
中, ,且
,且 ,则
,则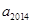 的值为 .
的值为 . 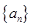 中,
中,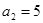 ,
,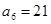 ,记数列
,记数列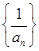 的前
的前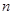 项和为
项和为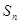 ,若
,若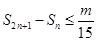 对
对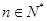 恒成立,则正整数
恒成立,则正整数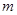 的最小值为( )
的最小值为( ) 中,已知
中,已知 ,则
,则 的值为 .
的值为 .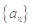 的前
的前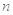 项和为
项和为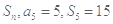 ,则数列
,则数列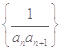 的前100项和为
的前100项和为 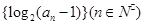 是等差数列,且
是等差数列,且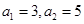 ,则
,则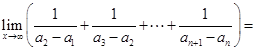 ( )
( )