题目内容
【题目】如图,已知抛物线![]() 焦点为
焦点为![]() ,直线
,直线![]() 经过点
经过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() ,
,![]() 两点
两点

(Ⅰ)若线段![]() 的中点在直线
的中点在直线![]() 上,求直线
上,求直线![]() 的方程;
的方程;
(Ⅱ)若线段![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)设直线l的斜率为k,A(x1,y1),B(x2,y2),AB的中点M(x0,y0),由点差法,可得2y0k=4,又![]() ,所以
,所以![]() 。(2)设直线l的方程为x=my+1,与抛物线联立组方程组,由弦长公式与志达定理,可求得参数m的值.
。(2)设直线l的方程为x=my+1,与抛物线联立组方程组,由弦长公式与志达定理,可求得参数m的值.
试题解析:(1)由已知得抛物线的焦点为F(1,0).因为线段AB的中点在直线y=2上,所以直线l的斜率存在,设直线l的斜率为k,A(x1,y1),B(x2,y2),AB的中点M(x0,y0),
则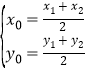 由
由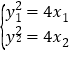 得
得
(y1+y2)(y1-y2)=4(x1-x2),所以2y0k=4.
又y0=2,所以k=1,故直线l的方程是y=x-1.
(2)设直线l的方程为x=my+1,与抛物线方程联立得![]() 消元得y2-4my-4=0,所以y1+y2=4m,y1y2=-4,Δ=16(m2+1)>0.
消元得y2-4my-4=0,所以y1+y2=4m,y1y2=-4,Δ=16(m2+1)>0.
|AB|=![]() |y1-y2|=
|y1-y2|=![]() ·
·![]()
=![]() ·
·![]() =4(m2+1).
=4(m2+1).
所以4(m2+1)=20,解得m=±2,
所以直线l的方程是x=±2y+1,
即x±2y-1=0.

【题目】为了推行“智慧课堂”教学,某老师分别用传统教学和“智慧课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期屮考试后,分别从两个班级屮各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以上统计数据填写下面![]() 列联表,并判断“成绩优良与教学方式是否有关”?
列联表,并判断“成绩优良与教学方式是否有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
| p>成绩不优良 | |||
总计 |
附: 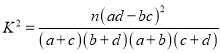 .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采川分层扣样的方法扣取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
