题目内容
定义在R上的函数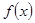 的图像如图所示,则关于
的图像如图所示,则关于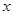 的不等式
的不等式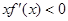 的解集为( )
的解集为( )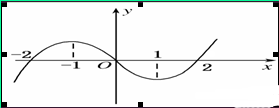
| A.(-2,-1)∪(1,2) | B.(-1,0)∪(1,+∞) |
| C.(-∞,-1)∪(0,1) | D.(-∞,-2)∪(2,+∞) |
C
解析试题分析:有图形可知:当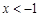 或
或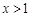 时,
时, 当
当 时,
时,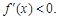 由
由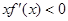 得
得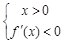 或
或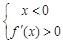 ,即
,即 或
或 或
或 ,因此
,因此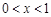 或
或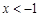 .
.
考点:导函数的几何意义

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
函数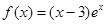 的单调递增区间是( )
的单调递增区间是( )
A.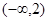 | B.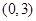 | C.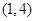 | D.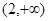 |
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
已知函数 在
在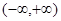 上是单调函数,则实数
上是单调函数,则实数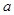 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
曲线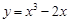 在
在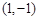 处的切线方程为( )
处的切线方程为( )
A.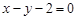 | B.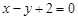 | C.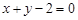 | D.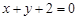 |
过抛物线y=x2上的点M(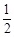 ,
, )的切线的倾斜角是( )
)的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
若函数 的导函数在区间
的导函数在区间 上的图像关于直线
上的图像关于直线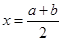 对称,则函数
对称,则函数 在区间
在区间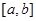 上的图象可能是( )
上的图象可能是( )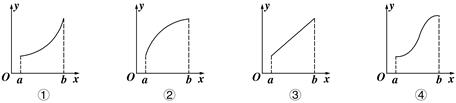
| A.①④ | B.②④ | C.②③ | D.③④ |
曲线y=-x3+3x2在点(1,2)处的切线方程为 ( ).
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |
曲线y=-x3+3x2在点(1,2)处的切线方程为( )
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |