题目内容
（2006•南京一模）已知A（-1，0），B（2，1），C（1，-1）．若将坐标平面沿x轴折成直二面角，则折后∠BAC的余弦值为
．
| 3 |
| 5 |
| 2 |
| 3 |
| 5 |
| 2 |
分析：先画出折叠前与折叠后的图形，再根据直二面角，求出三角形的三边长，运用余弦定理求解即可．
解答：解：如图
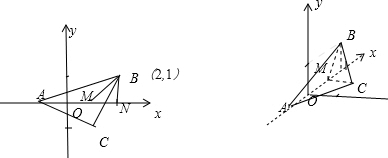
过C作CM⊥x轴，垂足为M，过B作BN⊥x轴，垂足为N，连接BM，
∵B（2，1），C（1，-1），
∴BN=1，MN=1．BM=
，
∵直二面角，∴CM⊥平面ABM，又BM?平面ABM，
∴BM⊥CM，BM=
，CM=1
∴BC=
AB=
，AC=
，
在△ABC中，根据余弦定理cos∠BAC=
=
．
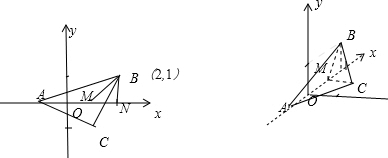
过C作CM⊥x轴，垂足为M，过B作BN⊥x轴，垂足为N，连接BM，
∵B（2，1），C（1，-1），
∴BN=1，MN=1．BM=
| 2 |
∵直二面角，∴CM⊥平面ABM，又BM?平面ABM，
∴BM⊥CM，BM=
| 2 |
∴BC=
| 3 |
AB=
| 10 |
| 5 |
在△ABC中，根据余弦定理cos∠BAC=
| 10+5-3 | ||||
2×
|
3
| ||
| 5 |
点评：本题考查面面垂直的性质及余弦定理．
练习册系列答案
相关题目