题目内容
已知
，（其中
）
（1）求
及
；
（2）试比较
与
的大小，并说明理由．
（1）
, 
（2）当
或
时，
;当
时，
．
解析试题分析：（1）根据题目特点，找特殊值
和
代入即可求解；（2）分析题目特点，等价代换比较大小：
与
，然后运用数学归纳法证明，先假设
时结论成立，证明的第二步，即
时，通过推理论证：成立.
（1）取，则；取，则
，．
（2）要比较与 的大小，即比较：与的大小，
当时，；
当时，；
当
时，；
猜想：当时，，下面用数学归纳法证明：
由上述过程可知，
时结论成立，
假设当时结论成立，即
，
两边同乘以
得：
＝
∵
时，
，
∴
∴
．
即时结论也成立，
∴当时，成立.
综上得，当或时，；
当时，．
考点：数学归纳法及推理论证.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(用含有
的式子表示，其中
为三角形
的三边，求证：
≤
.
，
，
．
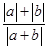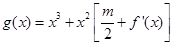时，试比较
与
的大小关系；
与
的大小关系，并给出证明．
计算
由此推测出
的计算公式，并用数学归纳法证明.
，
,
，
，则第5个等式为 ，…,推广到第
个等式为__ _；（注意：按规律写出等式的形式，不要求计算结果．）