题目内容
直线l过点(1,2)和第一、二、四象限,若直线l的横截距与纵截距之和为6,求直线l的方程.
解:设直线l的横截距为a,由题意可得纵截距为6-a,
∴直线l的方程为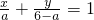 ,
,
∵点(1,2)在直线l上,
∴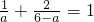 ,
,
解得:a1=2,a2=3,
当a=2时,直线的方程为2x+y-4=0,直线经过第一、二、四象限;
当a=3时,直线的方程为x+y-3=0,直线经过第一、二、四象限.
综上所述,所求直线方程为2x+y-4=0或x+y-3=0.
分析:设直线l的横截距为a,则纵截距为(6-a),写出直线l的截距式方程,把(1,2)代入即可求出a的值,把a的值代入直线l的方程中,经过检验得到满足题意的直线l的方程.
点评:此题考查学生会利用待定系数法求直线的截距式方程,是一道基础题.学生做题时应注意求得的a值有两个都满足题意.
∴直线l的方程为
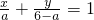 ,
,∵点(1,2)在直线l上,
∴
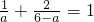 ,
,解得:a1=2,a2=3,
当a=2时,直线的方程为2x+y-4=0,直线经过第一、二、四象限;
当a=3时,直线的方程为x+y-3=0,直线经过第一、二、四象限.
综上所述,所求直线方程为2x+y-4=0或x+y-3=0.
分析:设直线l的横截距为a,则纵截距为(6-a),写出直线l的截距式方程,把(1,2)代入即可求出a的值,把a的值代入直线l的方程中,经过检验得到满足题意的直线l的方程.
点评:此题考查学生会利用待定系数法求直线的截距式方程,是一道基础题.学生做题时应注意求得的a值有两个都满足题意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线l过点(-1,2)且与直线2x-3y+9=0垂直,则l的方程是( )
| A、3x+2y-1=0 | B、3x+2y+7=0 | C、2x-3y+5=0 | D、2x-3y+8=0 |
已知直线l过点(-1,2)且与直线y=
x垂直,则直线l的方程是( )
| 2 |
| 3 |
| A、3x+2y-1=0 |
| B、3x+2y+7=0 |
| C、2x-3y+5=0 |
| D、2x-3y+8=0 |
已知直线l过点(1,2),且在x轴截距是在y轴截距的2倍,则直线l的方程为( )
| A、x+2y-5=0 | B、x+2y+5=0 | C、2x-y=0或x+2y-5=0 | D、2x-y=0或x-2y+3=0 |