题目内容
有下列四个命题,其中真命题有( )
①{an}为等比数列,则a1+a5≤a2+a4;
②{an}为等差数列,则a1•a5≤a2•a4;
③对任意α,β,都有sin(α+β)sin(α-β)=sin2α-sin2β;
④对任意α,β,都有cos(α+β)≠cosα+cosβ.
①{an}为等比数列,则a1+a5≤a2+a4;
②{an}为等差数列,则a1•a5≤a2•a4;
③对任意α,β,都有sin(α+β)sin(α-β)=sin2α-sin2β;
④对任意α,β,都有cos(α+β)≠cosα+cosβ.
分析:通过给变量取特殊值,举反例可得①④不正确,根据 a2•a4 -a1•a5 =3d2≥0,可得②正确.
利用两角和的正弦公式、同角三角函数基本关系化简sin(α+β)sin(α-β)=sin2α-sin2β,故③正确.
利用两角和的正弦公式、同角三角函数基本关系化简sin(α+β)sin(α-β)=sin2α-sin2β,故③正确.
解答:解:①不正确,如 an =
时,a1+a5 =
,a2+a4 =
.
②正确,因为 a2•a4 -a1•a5 =3d2≥0.
③正确,因为sin(α+β)sin(α-β)=(sinαcosβ+cosαsinβ)(sinαcosβ-cosαsinβ)
=sin2αcos2β-cos2αsin2β=sin2α(1-sin2β)-(1-sin2α)sin2β=sin2α-sin2β.
④不正确,如α =
, β =-
时,cos(α+β)=1,cosα+cosβ=
+
=1.
故②③正确,①④不正确.
故选B.
| 1 |
| 2n-1 |
| 17 |
| 16 |
| 5 |
| 8 |
②正确,因为 a2•a4 -a1•a5 =3d2≥0.
③正确,因为sin(α+β)sin(α-β)=(sinαcosβ+cosαsinβ)(sinαcosβ-cosαsinβ)
=sin2αcos2β-cos2αsin2β=sin2α(1-sin2β)-(1-sin2α)sin2β=sin2α-sin2β.
④不正确,如α =
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
故②③正确,①④不正确.
故选B.
点评:本题主要考查等差数列的定义和性质、等比数列的定义和性质,两角和的正弦公式.通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
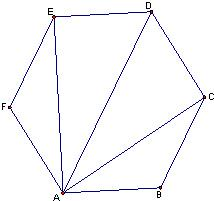 如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是
如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是