题目内容
有下列四个命题,其中真命题有( )
①若x2+y2≠0,则x,y都不为0;
②“若q<2,则x2+2x+q=0有实根”的逆命题;
③“全等三角形的面积相等”的否命题;
④“对于正数a,若a>1,则lga>0”的逆否命题.
①若x2+y2≠0,则x,y都不为0;
②“若q<2,则x2+2x+q=0有实根”的逆命题;
③“全等三角形的面积相等”的否命题;
④“对于正数a,若a>1,则lga>0”的逆否命题.
分析:根据命题的条件与结论之间的关系及命题的逆命题,否命题,逆否命题的定义来判断,
可以利用命题的真假判断其逆否命题的真假.
可以利用命题的真假判断其逆否命题的真假.
解答:解:∵x2+y2≠0,x、y可一个为0另一个不为0,故①假命题;
∵x2+2x+q=0有根的条件是:4-4q≥0⇒q≤1,q<2成立,故②真命题;
∵否命题:不全等的三角形的面积不相等,∴③假命题;
∵a>1,则lga>0成立,∴命题为真命题,又∵命题与其逆否命题同真,同假,∴④真命题;
故选D
∵x2+2x+q=0有根的条件是:4-4q≥0⇒q≤1,q<2成立,故②真命题;
∵否命题:不全等的三角形的面积不相等,∴③假命题;
∵a>1,则lga>0成立,∴命题为真命题,又∵命题与其逆否命题同真,同假,∴④真命题;
故选D
点评:本题考查四种命题的真假判定,要注意利用命题与其逆否命题同真、同假来判定.

练习册系列答案
相关题目
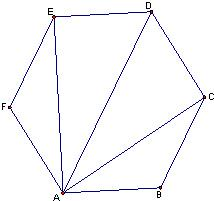 如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是
如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是