题目内容
关于数列有下列四个命题,其中正确命题的序号是
①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}既是等差数列又是等比数列,则an=an+1;
③数列{an}的前n项和为Sn,且Sn=an-1(a∈R),则{an}为等比数列;
④数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n)
②④
②④
.①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}既是等差数列又是等比数列,则an=an+1;
③数列{an}的前n项和为Sn,且Sn=an-1(a∈R),则{an}为等比数列;
④数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n)
分析:①利用特殊数列-1,1,-1,1,进行验证.②利用等差数列和等比数列的定义进行判断.③当a=0时,进行排除判断.④利用等差数列的通项公式进行判断.
解答:解:①对于数列-1,1,-1,1,满足a,b,c,d成等比数列,但a+b=0,b+c=0,c+d=0,所以a+b,b+c,c+d不是等比数列,所以①错误.
②若数列{an}既是等差数列又是等比数列,则数列{an}必是非零的常数列,所以an=an+1成立,所以②正确.
③当a=0时,数列{an}既不是等差数列也不是等比数列,所以③错误.
④在等差数列中,若am=an,则a1+(m-1)d=a1+(n-1)d,因为d≠0,所以m=n,与m≠n矛盾,所以④正确.
故答案为:②④.
②若数列{an}既是等差数列又是等比数列,则数列{an}必是非零的常数列,所以an=an+1成立,所以②正确.
③当a=0时,数列{an}既不是等差数列也不是等比数列,所以③错误.
④在等差数列中,若am=an,则a1+(m-1)d=a1+(n-1)d,因为d≠0,所以m=n,与m≠n矛盾,所以④正确.
故答案为:②④.
点评:本题主要考查等差数列和等比数列的定义和通项公式,比较基础.

练习册系列答案
相关题目
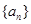 的前
的前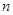 项和为
项和为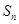 ,关于数列
,关于数列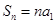 ;
;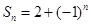 ,则
,则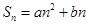
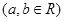 ,则
,则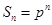 ,则无论
,则无论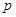 取何值时
取何值时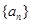 的前
的前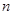 项和为
项和为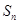 ,关于数列
,关于数列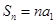 ;
;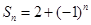 ,则
,则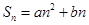
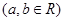 ,则
,则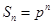 ,则无论
,则无论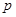 取何值时
取何值时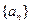 的前
的前 项和为
项和为 ,关于数列
,关于数列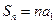 ;
;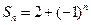 ,则
,则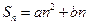
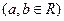 ,则
,则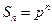 ,则无论
,则无论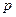 取何值时
取何值时 数列。其中正确命题的序号是
数列。其中正确命题的序号是 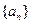 的前
的前 项和为
项和为 ,关于数列
,关于数列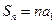 ;
; ,则
,则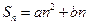
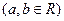 ,则
,则
 ,则无论
,则无论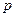 取何值时
取何值时 ;
;