题目内容
设抛物线C:y2=2px(p>0)的焦点到准线的距离是2.
(Ⅰ)求此抛物线方程;
(Ⅱ)设点A,B在此抛物线上,点F为此抛物线的焦点,且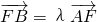 ,若λ∈[4,9],求直线AB在y轴上截距的取值范围.
,若λ∈[4,9],求直线AB在y轴上截距的取值范围.
解:(Ⅰ)因为抛物线C:y2=2px(p>0)的焦点到准线的距离p=2
所以此抛物线方程为y2=4x
(Ⅱ)由题意,直线AB的斜率存在.F(1,0),设直线AB的方程为y=k(x-1)
由 消y,整理得,k2x2-(2k2+4)x+k2=0
消y,整理得,k2x2-(2k2+4)x+k2=0
△=(2k2+4)2-4k4=16k2+16>0,
设A(x1,y1),B(x1,y1)则 ,x1•x2=1
,x1•x2=1
因为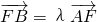 ,所以(x2-1,y2)=λ(1-x1,-y1),于是
,所以(x2-1,y2)=λ(1-x1,-y1),于是
由y2=-λy1,得y22=λ2y12?4x2=λ2•4x1?x2=λ2•x1,
又x1•x2=1,
消x2得λ2•x12=1,
因为x1>0,所以 ,从而,x2=λ.
,从而,x2=λ.
代入 得,
得, ,
,
令 ,
,
因为 在[4,9]上递增,
在[4,9]上递增,
所以 ,即
,即 ,
,
于是, ,或
,或
所以直线AB在y轴上截距的取值范围为: .
.
分析:(Ⅰ)根据焦点到准线的距离求得p,则抛物线方程可得.
(Ⅱ)设出直线AB的方程与抛物线方程联立消去y,设A(x1,y1),B(x1,y1)根据韦达定理可表示出x1+x2和x1•x2,根据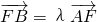 ,进而求得x2=λ2•x1,进而根据x1•x2=1,消去x2,求得x1和x2,代入x1+x2中,求得λ和k的关系式,根据
,进而求得x2=λ2•x1,进而根据x1•x2=1,消去x2,求得x1和x2,代入x1+x2中,求得λ和k的关系式,根据 在[4,9]上递增,进而求得y的范围进而求得k的范围,进而求得直线在x轴上的截距的范围可得.
在[4,9]上递增,进而求得y的范围进而求得k的范围,进而求得直线在x轴上的截距的范围可得.
点评:本题主要考查了抛物线的标准方程,直线与抛物线的关系,向量的计算等.考查了学生运用所学知识灵活解决问题的能力.
所以此抛物线方程为y2=4x
(Ⅱ)由题意,直线AB的斜率存在.F(1,0),设直线AB的方程为y=k(x-1)
由
 消y,整理得,k2x2-(2k2+4)x+k2=0
消y,整理得,k2x2-(2k2+4)x+k2=0△=(2k2+4)2-4k4=16k2+16>0,
设A(x1,y1),B(x1,y1)则
 ,x1•x2=1
,x1•x2=1因为
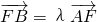 ,所以(x2-1,y2)=λ(1-x1,-y1),于是
,所以(x2-1,y2)=λ(1-x1,-y1),于是
由y2=-λy1,得y22=λ2y12?4x2=λ2•4x1?x2=λ2•x1,
又x1•x2=1,
消x2得λ2•x12=1,
因为x1>0,所以
 ,从而,x2=λ.
,从而,x2=λ.代入
 得,
得, ,
,令
 ,
,因为
 在[4,9]上递增,
在[4,9]上递增,所以
 ,即
,即 ,
,于是,
 ,或
,或
所以直线AB在y轴上截距的取值范围为:
 .
.分析:(Ⅰ)根据焦点到准线的距离求得p,则抛物线方程可得.
(Ⅱ)设出直线AB的方程与抛物线方程联立消去y,设A(x1,y1),B(x1,y1)根据韦达定理可表示出x1+x2和x1•x2,根据
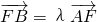 ,进而求得x2=λ2•x1,进而根据x1•x2=1,消去x2,求得x1和x2,代入x1+x2中,求得λ和k的关系式,根据
,进而求得x2=λ2•x1,进而根据x1•x2=1,消去x2,求得x1和x2,代入x1+x2中,求得λ和k的关系式,根据 在[4,9]上递增,进而求得y的范围进而求得k的范围,进而求得直线在x轴上的截距的范围可得.
在[4,9]上递增,进而求得y的范围进而求得k的范围,进而求得直线在x轴上的截距的范围可得.点评:本题主要考查了抛物线的标准方程,直线与抛物线的关系,向量的计算等.考查了学生运用所学知识灵活解决问题的能力.

练习册系列答案
相关题目