题目内容
已知数列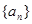 的前
的前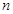 项的和为
项的和为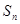 ,
, 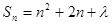 ,求证:数列
,求证:数列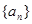 为等差数列的充要条件是
为等差数列的充要条件是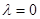 .
.
详见解析.
解析试题分析:从两个方面来证明此题:若数列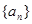 为等差数列,则其前
为等差数列,则其前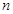 项和
项和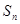 是关于
是关于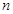 的二次函数,且常数项为
的二次函数,且常数项为 ,即
,即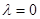 ;若
;若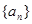 的前
的前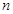 项和
项和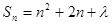 中
中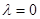 ,可根据其前
,可根据其前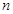 项和
项和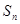 求出通项公式,从而可以证明其为等差数列.
求出通项公式,从而可以证明其为等差数列.
试题解析:证:若数列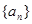 为等差数列,则其前
为等差数列,则其前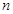 项和
项和 ,
,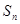 是关于
是关于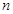 的二次函数,且常数项为
的二次函数,且常数项为 ,而
,而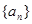 的前
的前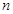 项和
项和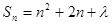 ,所以
,所以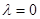 ;
;
反过来,当数列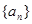 的前
的前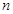 项和
项和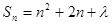 中
中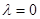 ,则
,则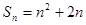 ,当
,当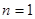 时,
时,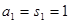 ,
,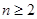 时,
时, ,因为
,因为 也符合
也符合 ,所以数列
,所以数列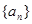 的通项公式为
的通项公式为 ,
,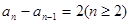 ,所以数列
,所以数列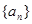 是以
是以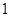 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
综上所述,数列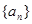 为等差数列的充要条件是
为等差数列的充要条件是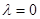 .
.
考点:本题主要考查了等差数列的前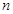 项和公式以及充分必要条件的关系.
项和公式以及充分必要条件的关系.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
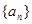 是等差数列,
是等差数列,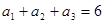 ,
,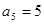 .
.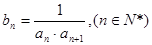 ,求数列
,求数列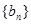 的前
的前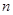 项和
项和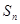 .
. 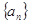 中,
中,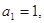 且点
且点 在直线
在直线 上。
上。 的通项公式;
的通项公式;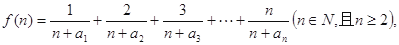 求函数
求函数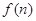 的最小值;
的最小值; 表示数列
表示数列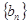 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式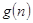 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 ,
, ,
,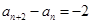
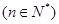
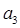

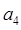 ,并求数列{an}通项公式;
,并求数列{an}通项公式; ,当
,当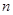 的值.
的值. 的首项
的首项 ,
, ,前
,前 项和为
项和为 .
. 及
及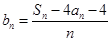 ,
, ,求
,求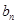 的最大值.
的最大值.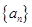 的公差
的公差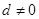 ,它的前
,它的前 项和为
项和为 ,若
,若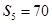 ,且
,且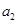 、
、 、
、 成等比数列.
成等比数列. 的前
的前 ,求证:
,求证: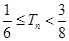 .
. 成等比数列.
成等比数列.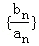 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.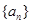 的首项
的首项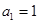 ,公差
,公差 .且
.且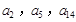 分别是等比数列
分别是等比数列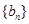 的
的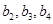 .
.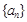 与
与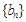 的通项公式;
的通项公式;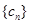 对任意自然数
对任意自然数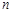 均有
均有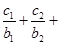
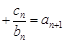 成立,求
成立,求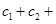
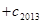 的值.
的值. 满足:
满足: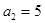 ,
,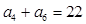 .
. .
.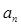 及
及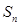 ;
;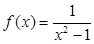 ,
,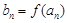 (
(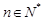 ),求数列
),求数列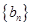 的前
的前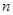 项和
项和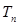 .
.