题目内容
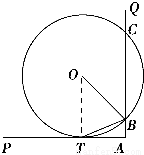
如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C.求证：BT平分∠OBA.
见解析
【解析】
证明 连接OT，因为AT是切线，所以OT⊥AP.
又因为∠PAQ是直角，即AQ⊥AP，
所以AB∥OT，
所以∠TBA＝∠BTO.
又OT＝OB，所以∠OTB＝∠OBT，
所以∠OBT＝∠TBA，即BT平分∠OBA.
练习册系列答案
相关题目
题目内容
如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C.求证：BT平分∠OBA.
见解析
【解析】
证明 连接OT，因为AT是切线，所以OT⊥AP.
又因为∠PAQ是直角，即AQ⊥AP，
所以AB∥OT，
所以∠TBA＝∠BTO.
又OT＝OB，所以∠OTB＝∠OBT，
所以∠OBT＝∠TBA，即BT平分∠OBA.
