题目内容
1.已知F1、F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的左右两个焦点,过F2且斜率为1的直线l交椭圆于A、B两点.(Ⅰ)求直线l的方程及△AF1B的周长;
(Ⅱ)求线段|AB|的长.
分析 (Ⅰ)求得双曲线的a,b,c,右焦点,可得直线的方程y=x-$\sqrt{7}$,代入双曲线的方程,运用韦达定理和弦长公式,可得|AB|,再由双曲线的定义可得△AF1B的周长为4a+2|AB|=8+2|AB|,计算即可得到;
(Ⅱ)由(Ⅰ)即可得到弦长.
解答 解:(Ⅰ)双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的a=2,b=$\sqrt{3}$,c=$\sqrt{7}$,
右焦点F2($\sqrt{7}$,0),即有直线l的方程为y=x-$\sqrt{7}$,
代入双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1,可得x2-8$\sqrt{7}$x+40=0,
即有x1+x2=8$\sqrt{7}$,x1x2=40,
则A,B为右支上的两点,
设|AF2|=m,|BF2|=n,则|AF1|=2a+m,|BF1|=2a+n,
即有△AF1B的周长为4a+2|AB|=8+2|AB|,
由弦长公式可得|AB|=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}$•$\sqrt{(8\sqrt{7})^{2}-4×40}$=24,
即有△AF1B的周长为8+48=56;
(Ⅱ)由(Ⅰ)可得|AB|=24.
点评 本题考查双曲线的定义、方程的运用,考查直线和双曲线联立方程,运用韦达定理和弦长公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
11.已知2-ai=b+i(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
11.已知方程x=3-lgx,下列说法正确的是( )
| A. | 方程x=3-lgx的解在区间(0,1)内 | B. | 方程x=3-lgx的解在区间(1,2)内 | ||
| C. | 方程x=3-lgx的解在区间(2,3)内 | D. | 方程x=3-lgx的解在区间(3,4)内 |
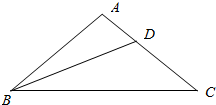 △ABC中,AD:DC=5:9,△ABD的面积为22.5cm2,那么△BDC的面积是多少?△ABC的面积是多少?
△ABC中,AD:DC=5:9,△ABD的面积为22.5cm2,那么△BDC的面积是多少?△ABC的面积是多少?