题目内容
下列命题:(1)若函数f(x)=lg(x+
 ),为奇函数,则a=1;
),为奇函数,则a=1;(2)函数f(x)=|sinx|的周期T=π;
(3)已知
 ,其中θ∈(π,
,其中θ∈(π, ),则
),则
(4)在△ABC中,
 =a,
=a, =b,若a•b<0,则△ABC是钝角三角形
=b,若a•b<0,则△ABC是钝角三角形( 5)O是△ABC所在平面上一定点,动点P满足:
 ,λ∈(0,+∞),则直线AP一定通过△ABC的内心.
,λ∈(0,+∞),则直线AP一定通过△ABC的内心.以上命题为真命题的是 .
【答案】分析:(1)若函数f(x)=lg(x+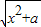 )为奇函数,则f(0)=0,则此能求出a的值;
)为奇函数,则f(0)=0,则此能求出a的值;
(2)由正弦函数的图象知函数能求出f(x)的周期;
(3)写出两个向量的数量积,运用同角三角函数的基本关系式整理即可得到结论;
(4)在△ABC中,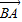 =
=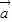 ,
,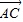 =
=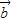 ,
,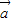 •
•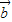 <0,则∠BAC是锐角,由此无法判断△ABC一定是钝角三角形;
<0,则∠BAC是锐角,由此无法判断△ABC一定是钝角三角形;
(5)把给出等式中的角的正弦值用对应边长和外接圆半径表示,移向整理后得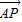 =2Rλ(
=2Rλ(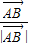 +
+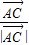 ),由此式可知直线AP一定通过△ABC的内心.
),由此式可知直线AP一定通过△ABC的内心.
解答:解:若函数f(x)=lg(x+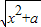 )为奇函数,
)为奇函数,
则f(0)=lg(0+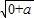 )=lg
)=lg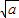 =0,解得a=1,故(1)成立;
=0,解得a=1,故(1)成立;
由正弦函数的图象知函数f(x)=|sinx|的周期T=π,故(2)成立;
∵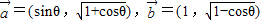 ,其中θ∈(π,
,其中θ∈(π,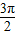 ),
),
∴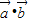 =sinθ+
=sinθ+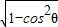 =sinθ-sinθ=0,
=sinθ-sinθ=0,
∴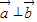 ,故(3)成立;
,故(3)成立;
在△ABC中,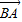 =
=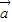 ,
,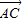 =
=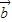 ,
,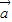 •
•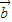 <0,
<0,
则∠BAC是锐角,△ABC不一定是钝角三角形,故(4)不成立;
如图,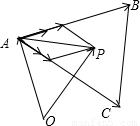
在△ABC中,由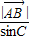 =
=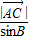 =2R(R为三角形ABC外接圆半径),
=2R(R为三角形ABC外接圆半径),
所以sinC=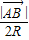 ,sinB=
,sinB=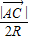 ,
,
所以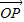 =
=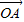 +λ(
+λ(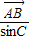 +
+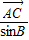 )=
)=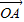 +λ(
+λ(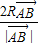 +
+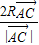 )=
)=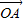 +2Rλ(
+2Rλ(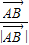 +
+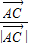 ),
),
即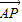 =2Rλ(
=2Rλ(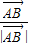 +
+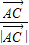 ),
),
所以直线AP一定通过△ABC的内心.故(5)正确.
故答案为:(1)(2)(3)(5).
点评:本题考查了命题的真假的判断与运用,是中档题.解题时要认真审题,注意奇函数、向量的数量积、三角函数、正弦定理等知识点的合理运用.
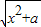 )为奇函数,则f(0)=0,则此能求出a的值;
)为奇函数,则f(0)=0,则此能求出a的值;(2)由正弦函数的图象知函数能求出f(x)的周期;
(3)写出两个向量的数量积,运用同角三角函数的基本关系式整理即可得到结论;
(4)在△ABC中,
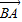 =
=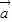 ,
,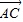 =
=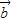 ,
,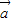 •
•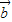 <0,则∠BAC是锐角,由此无法判断△ABC一定是钝角三角形;
<0,则∠BAC是锐角,由此无法判断△ABC一定是钝角三角形;(5)把给出等式中的角的正弦值用对应边长和外接圆半径表示,移向整理后得
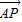 =2Rλ(
=2Rλ(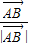 +
+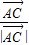 ),由此式可知直线AP一定通过△ABC的内心.
),由此式可知直线AP一定通过△ABC的内心.解答:解:若函数f(x)=lg(x+
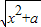 )为奇函数,
)为奇函数,则f(0)=lg(0+
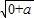 )=lg
)=lg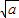 =0,解得a=1,故(1)成立;
=0,解得a=1,故(1)成立;由正弦函数的图象知函数f(x)=|sinx|的周期T=π,故(2)成立;
∵
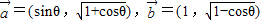 ,其中θ∈(π,
,其中θ∈(π,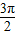 ),
),∴
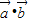 =sinθ+
=sinθ+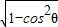 =sinθ-sinθ=0,
=sinθ-sinθ=0,∴
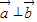 ,故(3)成立;
,故(3)成立;在△ABC中,
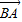 =
=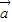 ,
,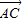 =
=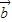 ,
,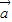 •
•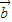 <0,
<0,则∠BAC是锐角,△ABC不一定是钝角三角形,故(4)不成立;
如图,

在△ABC中,由
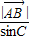 =
=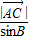 =2R(R为三角形ABC外接圆半径),
=2R(R为三角形ABC外接圆半径),所以sinC=
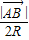 ,sinB=
,sinB=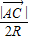 ,
,所以
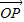 =
=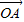 +λ(
+λ(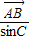 +
+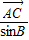 )=
)=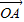 +λ(
+λ(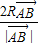 +
+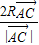 )=
)=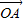 +2Rλ(
+2Rλ(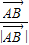 +
+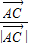 ),
),即
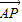 =2Rλ(
=2Rλ(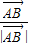 +
+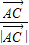 ),
),所以直线AP一定通过△ABC的内心.故(5)正确.
故答案为:(1)(2)(3)(5).
点评:本题考查了命题的真假的判断与运用,是中档题.解题时要认真审题,注意奇函数、向量的数量积、三角函数、正弦定理等知识点的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (0<x<1)的最大函数值为
(0<x<1)的最大函数值为 ;
; ≥
≥ .
.