题目内容
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球.
(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列和数学期望.
的分布列和数学期望.
 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球.(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设
 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列和数学期望.
的分布列和数学期望.(I)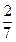 (II)
(II)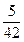 (III)
(III) 的分布列为:
的分布列为:
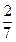 (II)
(II)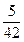 (III)
(III) 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
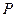 | 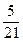 | 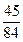 | 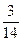 | 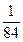 |
记“取出1个红色球,1个白色球,1个黑色球”为事件
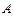 ,
, 则
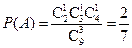 . ………….. 3分
. ………….. 3分(Ⅱ)解:
 记“取出1个红色球,2个白色球”为事件
记“取出1个红色球,2个白色球”为事件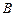 ,“取出2个红色球, 1个黑色球”为事件
,“取出2个红色球, 1个黑色球”为事件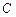 ,
,则
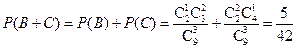 . ………….. 6分
. ………….. 6分(Ⅲ)解:
 可能的取值为
可能的取值为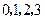 .
. 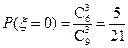 ,
, 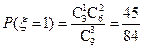 ,
,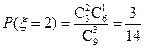 ,
, 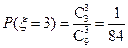 .
.  的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
 | 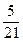 | 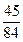 | 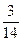 | 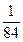 |
 的数学期望
的数学期望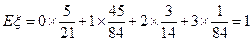 .
. 
练习册系列答案
相关题目
 (k=1,2,3,4):
(k=1,2,3,4): 的值;
的值; 的分布列;
的分布列; 的值.
的值. 表示所选3人中女生的人数.
表示所选3人中女生的人数. ”的概率.
”的概率.
 ,[50,60
,[50,60 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。(1)求
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。(1)求 (I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
(I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为 ,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,记
,记 .
. 的最大值,并求事件“
的最大值,并求事件“ 是一个随机变量,它的分布列如下:
是一个随机变量,它的分布列如下:
 ,则
,则 与
与 分别为( )
分别为( )