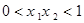题目内容
(本小题满分12分)
设函数y=f (x)=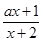 在区间 (-2,+∞)上单调递增,求a的取值范围.
在区间 (-2,+∞)上单调递增,求a的取值范围.
设函数y=f (x)=
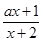 在区间 (-2,+∞)上单调递增,求a的取值范围.
在区间 (-2,+∞)上单调递增,求a的取值范围.a>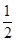 .
.
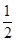 .
.本试题主要是考查了函数的单调性的运用。利用定义法来证明函数的 单调性,然后得到参数的取值范围。
解:设任意的x1,x2∈(-2,+∞),且x1<x2,
∵f(x1)-f(x2)=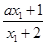 -
-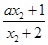 =
=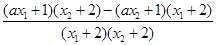
= .
.
∵f(x)在(-2,+∞)上单调递增,
∴f(x1)-f(x2)<0.∴ <0,
<0,
∵x1-x2<0,x1+2>0,x2+2>0,∴2a-1>0,∴a>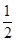 .
.
解:设任意的x1,x2∈(-2,+∞),且x1<x2,
∵f(x1)-f(x2)=
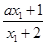 -
-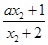 =
=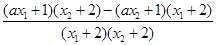
=
 .
.∵f(x)在(-2,+∞)上单调递增,
∴f(x1)-f(x2)<0.∴
 <0,
<0,∵x1-x2<0,x1+2>0,x2+2>0,∴2a-1>0,∴a>
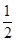 .
.
练习册系列答案
相关题目
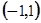 的函数
的函数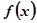
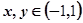 都有
都有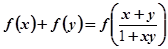 ;
;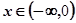 时,
时,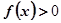 ,回答下列问题:
,回答下列问题: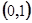 的单调性,并说明理由;
的单调性,并说明理由;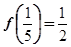 ,求
,求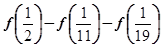 的值.
的值. 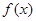 的定义域为D,若对于任意
的定义域为D,若对于任意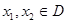 ,当
,当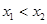 时,都有
时,都有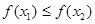 ,则称函数
,则称函数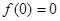 ;②
;② 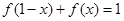
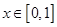 ; ③ 当
; ③ 当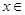
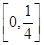 时,
时,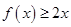 恒成立.则
恒成立.则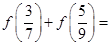 .
.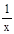
 -2x
-2x 
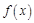 是奇函数,且在区间
是奇函数,且在区间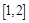 上单调递减,则
上单调递减,则 上是( )
上是( ) 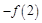
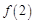
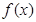 是定义在R上的偶函数,且对于任意的
是定义在R上的偶函数,且对于任意的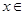 R都有
R都有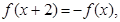 若当
若当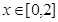 时,
时,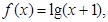 则有( )
则有( )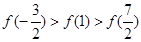
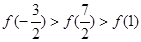

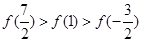
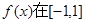 上是单调函数,且
上是单调函数,且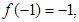 若函数
若函数 对所有的
对所有的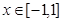 都成立,当
都成立,当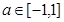 时,则
时,则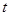 的取值范围是
的取值范围是 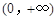 上的函数
上的函数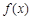 满足:对任意
满足:对任意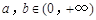 ,都有
,都有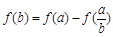 ,且当
,且当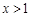 时,
时,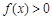 .
.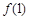 的值;
的值; ,解不等式
,解不等式 .
.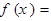
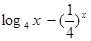 、
、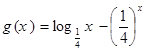 的零点分别为
的零点分别为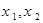 ,则( )
,则( )