题目内容
(2012•顺河区一模)设函数f(x)=sin2x-sin(2x-
).
(I)求函数f(x)的最小正周期和最大值;
(Ⅱ)△ABC的内角A.B、C的对边分别为a、b、c,c=3,f(
)=
,若向量
=(1,sinA)与
=(2,sinB)共线,求a,b的值.
| π |
| 2 |
(I)求函数f(x)的最小正周期和最大值;
(Ⅱ)△ABC的内角A.B、C的对边分别为a、b、c,c=3,f(
| C |
| 2 |
| 1 |
| 4 |
| m |
| n |
分析:(I)利用二倍角公式化简函数,即可求函数f(x)的最小正周期和最大值;
(Ⅱ)确定C的值,利用向量知识及余弦定理,可得结论.
(Ⅱ)确定C的值,利用向量知识及余弦定理,可得结论.
解答:解:(I)f(x)=sin2x-sin(2x-
)=
+cos2x=
∴T=
=π
当cos2x=1时,函数取得最大值1;
(Ⅱ)∵f(
)=
,∴
=
,
又∵C∈(0,π),∴C=
∵
=(1,sinA)与
=(2,sinB)共线
∴sinB=2sinA
∴b=2a
∵c=3
∴9=a2+4a2-2a×2a×cos
∴a=
∴b=
.
| π |
| 2 |
| 1-cos2x |
| 2 |
| 1+cos2x |
| 2 |
∴T=
| 2π |
| 2 |
当cos2x=1时,函数取得最大值1;
(Ⅱ)∵f(
| C |
| 2 |
| 1 |
| 4 |
| 1+cosC |
| 2 |
| 1 |
| 4 |
又∵C∈(0,π),∴C=
| 2π |
| 3 |
∵
| m |
| n |
∴sinB=2sinA
∴b=2a
∵c=3
∴9=a2+4a2-2a×2a×cos
| 2π |
| 3 |
∴a=
3
| ||
| 7 |
∴b=
6
| ||
| 7 |
点评:本题考查三角函数的化简,考查三角函数的性质,考查向量知识,考查余弦定理的运用,属于中档题.

练习册系列答案
相关题目
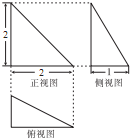 (2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )
(2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )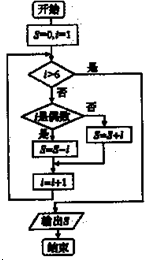 (2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )
(2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )