题目内容
已知二次函数f(x)=ax2+bx+c.(1)若f(-1)=0,试判断函数f(x)零点个数;
(2)若对?x1,x2∈R,且x1<x2,f(x1)≠f(x2),试证明?x∈(x1,x2),使
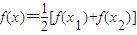 成立.
成立.(3)是否存在a,b,c∈R,使f(x)同时满足以下条件①对?x∈R,f(x-4)=f(2-x),且f(x)≥0;②对?x∈R,都有
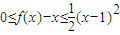 .若存在,求出a,b,c的值,若不存在,请说明理由.
.若存在,求出a,b,c的值,若不存在,请说明理由.
【答案】分析:(1)将x=-1代入得到关于a、b、c的关系式,再由△确定零点个数.
(2)令g(x)=f(x)-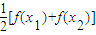 ,再由函数零点的判定定理可证.
,再由函数零点的判定定理可证.
(3)假设存在a,b,c∈R使得条件成立,由①可知函数f(x)的对称轴是x=-1,且最小值为0,由此可知a=c;由②知将x=1代入可求的a=c= ,b=
,b= ,最后验证即可.
,最后验证即可.
解答:解析:(1)∵f(-1)=0,
∴a-b+c=0,b=a+c
∵△=b2-4ac=(a+c)2-4ac=(a-c)2
当a=c时△=0,函数f(x)有一个零点;
当a≠c时,△>0,函数f(x)有两个零点.
(2)令 ,则
,则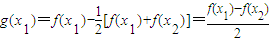
 ,
,
∴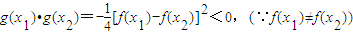
∴g(x)=0在(x1,x2)内必有一个实根.即?x∈(x1,x2),使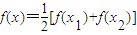 成立.
成立.
(3)假设a,b,c存在,由①知抛物线的对称轴为x=-1,且f(x)min=0
∴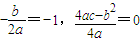 ⇒b=2a,b2=4ac⇒4a2=4ac⇒a=c
⇒b=2a,b2=4ac⇒4a2=4ac⇒a=c
由②知对?x∈R,都有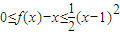
令x=1得0≤f(1)-1≤0⇒f(1)-1=0⇒f(1)=1⇒a+b+c=1
由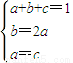 得
得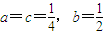 ,
,
当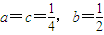 时,
时,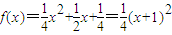 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又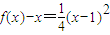 ⇒对?x∈R,都有
⇒对?x∈R,都有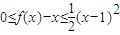 ,满足条件②.
,满足条件②.
∴存在a,b,c∈R,使f(x)同时满足条件①、②.
点评:本题主要考查函数零点的判断定理.
(2)令g(x)=f(x)-
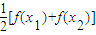 ,再由函数零点的判定定理可证.
,再由函数零点的判定定理可证.(3)假设存在a,b,c∈R使得条件成立,由①可知函数f(x)的对称轴是x=-1,且最小值为0,由此可知a=c;由②知将x=1代入可求的a=c=
 ,b=
,b= ,最后验证即可.
,最后验证即可.解答:解析:(1)∵f(-1)=0,
∴a-b+c=0,b=a+c
∵△=b2-4ac=(a+c)2-4ac=(a-c)2
当a=c时△=0,函数f(x)有一个零点;
当a≠c时,△>0,函数f(x)有两个零点.
(2)令
 ,则
,则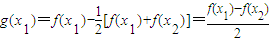
 ,
,∴
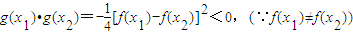
∴g(x)=0在(x1,x2)内必有一个实根.即?x∈(x1,x2),使
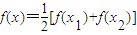 成立.
成立.(3)假设a,b,c存在,由①知抛物线的对称轴为x=-1,且f(x)min=0
∴
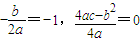 ⇒b=2a,b2=4ac⇒4a2=4ac⇒a=c
⇒b=2a,b2=4ac⇒4a2=4ac⇒a=c由②知对?x∈R,都有
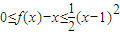
令x=1得0≤f(1)-1≤0⇒f(1)-1=0⇒f(1)=1⇒a+b+c=1
由
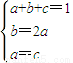 得
得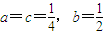 ,
,当
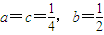 时,
时,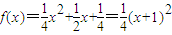 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又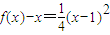 ⇒对?x∈R,都有
⇒对?x∈R,都有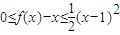 ,满足条件②.
,满足条件②.∴存在a,b,c∈R,使f(x)同时满足条件①、②.
点评:本题主要考查函数零点的判断定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目