题目内容
(2012•梅州二模)非空集合G关于运算⊕满足:(1)对于任意a、b∈G,都有a⊕b∈G;(2)存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,则称G关于运算⊕为“融洽集”,现在给出集合和运算::
①G={非负整数},⊕为整数的加法;
②G={偶数},⊕为整数的乘法;
③G={平面向量},⊕为平面向量的加法;
④G={虚数},⊕为复数乘法,其中G为关于运算⊕的“融洽集”的个数为( )
①G={非负整数},⊕为整数的加法;
②G={偶数},⊕为整数的乘法;
③G={平面向量},⊕为平面向量的加法;
④G={虚数},⊕为复数乘法,其中G为关于运算⊕的“融洽集”的个数为( )
分析:本题给出了新定义“融洽集”,判断给出的数集是否是“融洽集”,就要验证所给的数集是否满足“融洽集”,若其中有一个条件不满足,就不是“融洽集”.
解答:解:①对于任意非负整数a,b知道:a+b仍为非负整数,∴a⊕b∈G;取e=0,及任意飞负整数a,则a+0=0+a=a,因此G对于⊕为整数的加法运算来说是“融洽集”;
②对于任意偶数a,b知道:ab仍为偶数,故有a⊕b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故②的G不是“融洽集”.
③取任意向量
,
,则
+
仍为向量,故有a⊕b∈G;取
=
,及任意向量
,则
+
=
+
=
,故G是“融洽集”.
④取虚数a+bi与a-bi(其中b≠0),则(a+bi)(a-bi)=a2+b2为实数,也就是说不满足(a+bi)⊕(a-bi)∈G,
故④中的G不是“融洽集”.
故答案是B.
②对于任意偶数a,b知道:ab仍为偶数,故有a⊕b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故②的G不是“融洽集”.
③取任意向量
| a |
| b |
| a |
| b |
| e |
| 0 |
| a |
| a |
| 0 |
| 0 |
| a |
| a |
④取虚数a+bi与a-bi(其中b≠0),则(a+bi)(a-bi)=a2+b2为实数,也就是说不满足(a+bi)⊕(a-bi)∈G,
故④中的G不是“融洽集”.
故答案是B.
点评:本题考查了对新定义“融洽集”理解能力,及对有关知识的掌握情况.关键是看所给的数集是否满足“融洽集”的两个条件.

练习册系列答案
相关题目
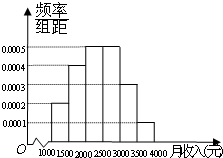 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).