题目内容
如图,在四棱锥 中,底面
中,底面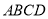 为正方形,侧面
为正方形,侧面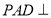 底面
底面 ,
, 为
为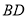 中点,
中点,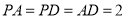 .
.
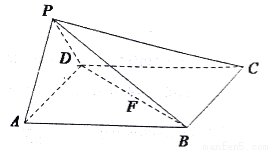
(I)在线段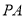 上是否存在点
上是否存在点 ,使得
,使得 //平面
//平面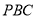 ,指出点
,指出点 的位置并证明;
的位置并证明;
(II)求二面角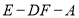 的余弦值.
的余弦值.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
题目内容
如图,在四棱锥 中,底面
中,底面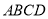 为正方形,侧面
为正方形,侧面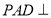 底面
底面 ,
, 为
为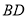 中点,
中点,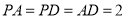 .
.

(I)在线段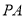 上是否存在点
上是否存在点 ,使得
,使得 //平面
//平面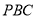 ,指出点
,指出点 的位置并证明;
的位置并证明;
(II)求二面角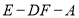 的余弦值.
的余弦值.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案