题目内容
已知正项等差数列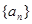 的前n项和为
的前n项和为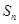 ,若
,若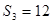 ,且
,且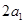 ,
,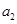 ,
,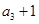 成等比数列,
成等比数列,
(1)求数列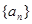 的通项公式;
的通项公式;
(2)设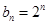 ,求数列
,求数列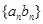 的前n项和
的前n项和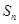 .
.
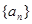 的前n项和为
的前n项和为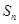 ,若
,若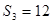 ,且
,且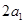 ,
,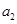 ,
,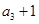 成等比数列,
成等比数列,(1)求数列
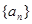 的通项公式;
的通项公式;(2)设
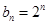 ,求数列
,求数列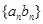 的前n项和
的前n项和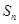 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)由等差数列的性质可知,
 ,再由
,再由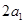 ,
,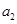 ,
,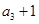 成等比数列,可得到关于公差
成等比数列,可得到关于公差 的方程:
的方程: ,再由
,再由 是正项等差数列可知
是正项等差数列可知 ,从而可得通项公式
,从而可得通项公式 ;(2)由(1)及
;(2)由(1)及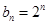 可知数列
可知数列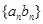 的通项公式为等差数列
的通项公式为等差数列 与等比数列
与等比数列 的乘积,因此可以考虑采用错位相减法来求其前
的乘积,因此可以考虑采用错位相减法来求其前 项和
项和 :
: ①,
①,①
 :
: ②,
②,①-②可得:

 ,即
,即 .
.试题解析:(1)∵等差数列
 ,
, ,∴
,∴ ,
, ,
,又∵
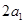 ,
,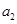 ,
,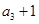 成等比数列,∴
成等比数列,∴ 或
或 ,
,又∵正项等差数列,∴
 ,∴
,∴ ;
;(2)∵
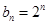 ,∴
,∴ ,
,∴
 ①,
①,①
 :
: ②,
②,①-②可得:

 ,
,∴
 .
.
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 中,
中, ,求数列
,求数列
 中,已知
中,已知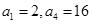 .
.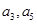 分别为等差数列
分别为等差数列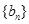 的第3项和第5项,试求数列
的第3项和第5项,试求数列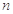 项和
项和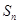 .
.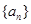 满足
满足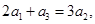 且
且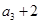 是
是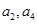 的等差中项
的等差中项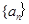 的通项公式;(2)若
的通项公式;(2)若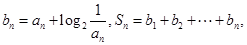 求使
求使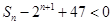 成立的正整数
成立的正整数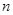 的最小值.
的最小值. 的通项公式
的通项公式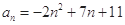 ,则该数列第________项最大.
,则该数列第________项最大. 的图像如下列图中,经过原点和(1,1),且对任意
的图像如下列图中,经过原点和(1,1),且对任意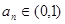 ,由关系式
,由关系式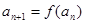 得到数列{
得到数列{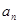 },满足
},满足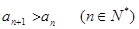 ,则该函数的图像为( )
,则该函数的图像为( )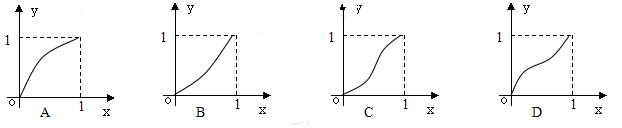
 的第15项为( )
的第15项为( ) 中,
中,
 ,则此数列前30项和等于( )
,则此数列前30项和等于( ) 中,
中, ,当
,当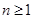 时,
时,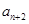 等于
等于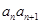 的个位数,则该数列的第2014项是
的个位数,则该数列的第2014项是