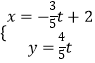ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ»ΐάβΧ®ABC©¹A1B1C1÷–Θ§ΤΫΟφΠΝΙΐΒψA1 Θ§ B1 Θ§ «“CC1ΓΈΤΫΟφΠΝΘ§ΤΫΟφΠΝ”κ»ΐάβΧ®ΒΡΟφœύΫΜΘ§ΫΜœΏΈß≥…“ΜΗωΥΡ±Ώ–ΈΘ°
Θ®ΔώΘ©‘ΎΆΦ÷–Μ≠≥ω’βΗωΥΡ±Ώ–ΈΘ§≤Δ÷Η≥ω «ΚΈ÷÷ΥΡ±Ώ–ΈΘ®≤Μ±ΊΥΒΟςΜ≠Ζ®ΓΔ≤Μ±ΊΥΒΟςΥΡ±Ώ–ΈΒΡ–ΈΉ¥Θ©ΘΜ
Θ®ΔρΘ©»τAB=8Θ§BC=2B1C1=6Θ§ABΓΆBCΘ§BB1=CC1 Θ§ ΤΫΟφBB1C1CΓΆΤΫΟφABCΘ§ΕΰΟφΫ«B1©¹AB©¹CΒ»”Ύ60ΓψΘ§«σ÷±œΏAB1”κΤΫΟφΠΝΥυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©Έß≥…ΒΡΥΡ±Ώ–Έ»γΆΦΥυ ΨΘ§Υϋ «ΤΫ––ΥΡ±Ώ–ΈΘΜΘ®ΔρΘ©ΓΏABΓΆBCΘ§ΤΫΟφBB1C1CΓΆΤΫΟφABCΘ§
«“ΤΫΟφBB1C1CΓΆΤΫΟφABC=BCΘ§ABΓ…ΤΫΟφABC
ΓύABΓΆΤΫΟφBB1C1CΘ§
ΓύABΓΆBB1 Θ§ ΓœB1BC «ΕΰΟφΫ«B1©¹AB©¹CΒΡΤΫΟφΫ«Θ§
ΓύΓœB1BC=60ΓψΘ§
“‘BCΘ§ABΈΣxΘ§y÷αΘ§BΈΣ‘≠ΒψΫ®ΝΔ»γΆΦ÷±Ϋ«Ήχ±ξœΒB©¹xyzΘ§
”…“―÷ΣCC1ΓΈΠΝΘ§B1M=ΠΝΓ…ΤΫΟφBB1C1CΘ§÷ΣB1MΓΈCC1 Θ§
”÷”…Χ®ΧεΒΡ–‘÷ Θ§BCΓΈB1C1 Θ§
ΓύMCC1B1 «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύMC=B1C1=3Θ§M «BCΒΡ÷–ΒψΘ§
”÷BB1=CC1 Θ§ ‘ρB1ΒΫΤΫΟφABCΒΡΨύάκΘ§h= ![]() Θ§
Θ§
Ά§άμN «ACΒΡ÷–ΒψΘ§
AΘ®0Θ§©¹8Θ§0Θ©Θ§BΘ®0Θ§0Θ§0Θ©Θ§B1Θ®©¹ ![]() Θ§0Θ§
Θ§0Θ§ ![]() Θ©Θ§MΘ®©¹3Θ§0Θ§0Θ©Θ§
Θ©Θ§MΘ®©¹3Θ§0Θ§0Θ©Θ§
‘ρ ![]() =Θ®
=Θ® ![]() Θ§0Θ§
Θ§0Θ§ ![]() Θ©Θ§
Θ©Θ§ ![]() =Θ®0Θ§©¹4Θ§0Θ©Θ§
=Θ®0Θ§©¹4Θ§0Θ©Θ§ ![]() =Θ®©¹
=Θ®©¹ ![]() Θ§8Θ§
Θ§8Θ§ ![]() Θ©Θ°
Θ©Θ°
…ηΤΫΟφΠΝΒΡΖ®œρΝΩΈΣ ![]() =Θ®xΘ§yΘ§zΘ©Θ§‘ρ
=Θ®xΘ§yΘ§zΘ©Θ§‘ρ 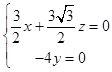
ΒΟ“ΜΗωΖ®œρΝΩ « ![]() =Θ®
=Θ® ![]() Θ§0Θ§©¹1Θ©Θ§
Θ§0Θ§©¹1Θ©Θ§
…η÷±œΏAB1”κΤΫΟφΠΝΥυ≥…Ϋ«ΈΣΠ»Θ§‘ρsinΠ»=|  |=
|= ![]() Θ°
Θ°
Γύ÷±œΏAB1”κΤΫΟφΠΝΥυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΈΣ ![]() Θ°
Θ°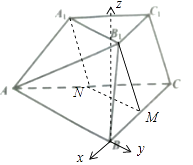
ΓΨΫβΈωΓΩΘ®ΔώΘ©Έß≥…ΒΡΥΡ±Ώ–Έ»γΆΦΥυ ΨΘ§Υϋ «ΤΫ––ΥΡ±Ώ–ΈΘΜΘ®ΔρΘ©“‘BCΘ§ABΈΣxΘ§y÷αΘ§BΈΣ‘≠ΒψΫ®ΝΔ»γΆΦ÷±Ϋ«Ήχ±ξœΒB©¹xyzΘ§«σ≥ωΤΫΟφΠΝΒΡΖ®œρΝΩΘ§άϊ”ΟœρΝΩΒΡΦ–Ϋ«ΙΪ ΫΘ§Φ¥Ω…«σ÷±œΏAB1”κΤΫΟφΠΝΥυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
ΓΨΩΦΒψΨΪΈωΓΩ»œ’φ…σΧβΘ§ Ήœ»–η“ΣΝΥΫβΤΫΟφΒΡΜυ±Ψ–‘÷ ΦΑΆΤ¬έ(»γΙϊ“ΜΧθ÷±œΏ…œΒΡΝΫΒψ‘Ύ“ΜΗωΤΫΟφΡΎΘ§Ρ«Ο¥’βΧθ÷±œΏ‘Ύ¥ΥΤΫΟφΡΎ;Ιΐ≤Μ‘Ύ“ΜΧθ÷±œΏ…œΒΡ»ΐΒψΘ§”–«“÷Μ”–“ΜΗωΤΫΟφ;»γΙϊΝΫΗω≤Μ÷ΊΚœΒΡΤΫΟφ”–“ΜΗωΙΪΙ≤ΒψΘ§Ρ«Ο¥ΥϋΟ«”–«“÷Μ”–“ΜΧθΙΐΗΟΒψΒΡΙΪΙ≤÷±œΏ)Θ§ΜΙ“Σ’ΤΈ’Ω’ΦδΫ«ΒΡ“λΟφ÷±œΏΥυ≥…ΒΡΫ«(“―÷Σ![]() ΈΣΝΫ“λΟφ÷±œΏΘ§AΘ§C”κBΘ§DΖ÷±π «
ΈΣΝΫ“λΟφ÷±œΏΘ§AΘ§C”κBΘ§DΖ÷±π «![]() …œΒΡ»Έ“βΝΫΒψΘ§
…œΒΡ»Έ“βΝΫΒψΘ§![]() Υυ≥…ΒΡΫ«ΈΣ
Υυ≥…ΒΡΫ«ΈΣ![]() Θ§‘ρ
Θ§‘ρ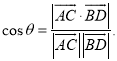 )ΒΡœύΙΊ÷Σ Ε≤≈ «¥πΧβΒΡΙΊΦϋΘ°
)ΒΡœύΙΊ÷Σ Ε≤≈ «¥πΧβΒΡΙΊΦϋΘ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ–ΓΟς‘Ύ ·Φ“Ή· –Ρ≥ΈοΝς≈…ΥΆΙΪΥΨ’“ΒΫΝΥ“ΜΖί≈…ΥΆ‘±ΒΡΙΛΉςΘ§ΗΟΙΪΥΨΗχ≥ωΝΥΝΫ÷÷»’–Ϋ–Ϋ≥ξΖΫΑΗΘ°ΦΉΖΫΑΗΘΚΒΉ–Ϋ100‘ΣΘ§ΟΩ≈…ΥΆ“ΜΒΞΫ±άχ1‘ΣΘΜ““ΖΫΑΗΘΚΒΉ–Ϋ140‘ΣΘ§ΟΩ»’«Α55ΒΞΟΜ”–Ϋ±άχΘ§≥§Ιΐ55ΒΞΒΡ≤ΩΖ÷ΟΩΒΞΫ±άχ12‘ΣΘ°
Θ®ΔώΘ©«κΖ÷±π«σ≥ωΦΉΓΔ““ΝΫ÷÷–Ϋ≥ξΖΫΑΗ÷–»’–ΫyΘ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΜθΒΞ ΐnΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®ΔρΘ©ΗυΨίΗΟΙΪΥΨΥυ”–≈…ΥΆ‘±100ΧλΒΡ≈…ΥΆΦ«¬ΦΘ§ΖΔœ÷≈…ΥΆ‘±ΒΡ»’ΤΫΨυ≈…ΥΆΒΞ ΐ¬ζΉψ“‘œ¬ΧθΦΰΘΚ‘Ύ’β100Χλ÷–ΒΡ≈…ΥΆΝΩ÷Η±ξ¬ζΉψ»γΆΦΥυ ΨΒΡ÷±ΖΫΆΦΘ§Τδ÷–Β±Ρ≥ΧλΒΡ≈…ΥΆΝΩ÷Η±ξ‘ΎΘ®![]() Θ§
Θ§![]() ]Θ®nΘΫ1Θ§2Θ§3Θ§4Θ§5Θ© ±Θ§»’ΤΫΨυ≈…ΥΆΝΩΈΣ50ΘΪ2nΒΞΘ°»τΫΪΤΒ¬ ”ΈΣΗ≈¬ Θ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
]Θ®nΘΫ1Θ§2Θ§3Θ§4Θ§5Θ© ±Θ§»’ΤΫΨυ≈…ΥΆΝΩΈΣ50ΘΪ2nΒΞΘ°»τΫΪΤΒ¬ ”ΈΣΗ≈¬ Θ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ

ΔΌΗυΨί“‘…œ ΐΨίΘ§…ηΟΩΟϊ≈…ΥΆ‘±ΒΡ»’–ΫΈΣXΘ®ΒΞΈΜΘΚ‘ΣΘ©Θ§ ‘Ζ÷±π«σ≥ωΦΉΓΔ““ΝΫ÷÷ΖΫΑΗΒΡ»’–ΫXΒΡΖ÷≤ΦΝ–Θ§ ΐ―ßΤΎΆϊΦΑΖΫ≤νΘΜ
ΔΎΫαΚœΔΌ÷–ΒΡ ΐΨίΘ§ΗυΨίΆ≥ΦΤ―ßΒΡΥΦœκΘ§Αο÷ζ–ΓΟςΖ÷ΈωΘ§Υϊ―Γ‘ώΡΡ÷÷–Ϋ≥ξΖΫΑΗ±»ΫœΚœ Θ§≤ΔΥΒΟςΡψΒΡάμ”…ΓΘ
Θ®≤ΈΩΦ ΐΨίΘΚ0Θ°62ΘΫ0Θ°36Θ§1Θ°42ΘΫ1Θ°9 6Θ§2Θ°6 2ΘΫ6Θ°76Θ§3Θ°42ΘΫ1 1Θ°56Θ§3Θ°62ΘΫ12Θ°96Θ§4Θ°62ΘΫ21Θ°16Θ§15Θ°62ΘΫ243Θ°36Θ§20Θ°42ΘΫ416Θ°16Θ§44Θ°42ΘΫ1971Θ°36Θ©
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©ΦΉΖΫΑΗΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ ![]() Θ§““ΖΫΑΗΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ
Θ§““ΖΫΑΗΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ![]() ΘΜΘ®ΔρΘ©ΔΌΦϊΫβΈωΘ§ΔΎΦϊΫβΈω.
ΘΜΘ®ΔρΘ©ΔΌΦϊΫβΈωΘ§ΔΎΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©”…Χβ“βΩ…ΒΟΦΉΖΫΑΗ÷–≈…ΥΆ‘±»’–Ϋ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ
Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ
ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ ![]() Θ§ ““ΖΫΑΗ÷–≈…ΥΆ‘±»’–Ϋ
Θ§ ““ΖΫΑΗ÷–≈…ΥΆ‘±»’–Ϋ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ
Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ
ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ![]() .
.
Θ®ΔρΘ©ΔΌ”…Χβ“β«σΒΟXΒΡΖ÷≤ΦΝ–Θ§Ψί¥ΥΦΤΥψΩ…ΒΟ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
ΔΎ¥πΑΗ“ΜΘΚ”…“‘…œΒΡΦΤΥψΩ…÷ΣΘ§![]() ‘Ε–Γ”Ύ
‘Ε–Γ”Ύ![]() Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ’»κ≤®Ε·œύΕ‘Ϋœ–ΓΘ§Υυ“‘–ΓΟς”Π―Γ‘ώΦΉΖΫΑΗ.
Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ’»κ≤®Ε·œύΕ‘Ϋœ–ΓΘ§Υυ“‘–ΓΟς”Π―Γ‘ώΦΉΖΫΑΗ.
¥πΑΗΕΰΘΚ”…“‘…œΒΡΦΤΥψΫαΙϊΩ…“‘Ω¥≥ωΘ§![]() Θ§Υυ“‘–ΓΟς”Π―Γ‘ώ““ΖΫΑΗ.
Θ§Υυ“‘–ΓΟς”Π―Γ‘ώ““ΖΫΑΗ.
Θ®ΔώΘ©ΦΉΖΫΑΗ÷–≈…ΥΆ‘±»’–Ϋ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ
Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ
ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ ![]() Θ§
Θ§
““ΖΫΑΗ÷–≈…ΥΆ‘±»’–Ϋ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ
Θ®ΒΞΈΜΘΚ‘ΣΘ©”κΥΆΒΞ ΐ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ
ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚ![]()
Θ®ΔρΘ©ΔΌ”…“―÷ΣΘ§‘Ύ’β100Χλ÷–Θ§ΗΟΙΪΥΨ≈…ΥΆ‘±»’ΤΫΨυ≈…ΥΆΒΞ ΐ¬ζΉψ»γœ¬±μΗώΘΚ
ΒΞ ΐ | 52 | 54 | 56 | 58 | 60 |
ΤΒ¬ | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
Υυ“‘![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
Υυ“‘![]()
Υυ“‘![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
Υυ“‘![]()
![]()
ΔΎ¥πΑΗ“ΜΘΚ”…“‘…œΒΡΦΤΥψΩ…÷ΣΘ§Υδ»Μ![]() Θ§ΒΪΝΫ’Ώœύ≤ν≤Μ¥σΘ§«“
Θ§ΒΪΝΫ’Ώœύ≤ν≤Μ¥σΘ§«“![]() ‘Ε–Γ”Ύ
‘Ε–Γ”Ύ![]() Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ’»κ≤®Ε·œύΕ‘Ϋœ–ΓΘ§Υυ“‘–ΓΟς”Π―Γ‘ώΦΉΖΫΑΗ.
Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ’»κ≤®Ε·œύΕ‘Ϋœ–ΓΘ§Υυ“‘–ΓΟς”Π―Γ‘ώΦΉΖΫΑΗ.
¥πΑΗΕΰΘΚ”…“‘…œΒΡΦΤΥψΫαΙϊΩ…“‘Ω¥≥ωΘ§![]() Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ΤΎΆϊ–Γ”Ύ““ΖΫΑΗ»’ΙΛΉ ΤΎΆϊΘ§Υυ“‘–ΓΟς”Π―Γ‘ώ““ΖΫΑΗ.
Θ§Φ¥ΦΉΖΫΑΗ»’ΙΛΉ ΤΎΆϊ–Γ”Ύ““ΖΫΑΗ»’ΙΛΉ ΤΎΆϊΘ§Υυ“‘–ΓΟς”Π―Γ‘ώ““ΖΫΑΗ.
ΓΨΒψΨΠΓΩ
±ΨΧβ÷ς“ΣΩΦ≤ιΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ ΐ―ßΤΎΆϊ”κΖΫ≤νΒΡΚ§“ε”κ ΒΦ ”Π”ΟΒ»÷Σ ΕΘ§“β‘ΎΩΦ≤ι―ß…ζΒΡΉΣΜ·ΡήΝΠΚΆΦΤΥψ«σΫβΡήΝΠ.
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
20
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΘΚ![]() Θ®aΘΨbΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§«“άκ–Ρ¬ ΈΣ
Θ®aΘΨbΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§«“άκ–Ρ¬ ΈΣ![]() Θ§MΈΣΆ÷‘≤…œ»Έ“β“ΜΒψΘ§Β±ΓœF1MF2ΘΫ90Γψ ±Θ§ΓςF1MF2ΒΡΟφΜΐΈΣ1Θ°
Θ§MΈΣΆ÷‘≤…œ»Έ“β“ΜΒψΘ§Β±ΓœF1MF2ΘΫ90Γψ ±Θ§ΓςF1MF2ΒΡΟφΜΐΈΣ1Θ°
Θ®ΔώΘ©«σΆ÷‘≤CΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©“―÷ΣΒψA «Ά÷‘≤C…œ“λ”ΎΆ÷‘≤ΕΞΒψΒΡ“ΜΒψΘ§―”≥Λ÷±œΏAF1Θ§AF2Ζ÷±π”κΆ÷‘≤ΫΜ”ΎΒψBΘ§DΘ§…η÷±œΏBDΒΡ–±¬ ΈΣk1Θ§÷±œΏOAΒΡ–±¬ ΈΣk2Θ§«σ÷ΛΘΚk1ΓΛk2Β»”ΎΕ®÷ΒΘ°
ΓΨΧβΡΩΓΩΈΣΝΥΫβΗΏ÷–…ζΉςΈΡ≥…Φ®”κΩΈΆβ‘ΡΕΝΝΩ÷°ΦδΒΡΙΊœΒΘ§Ρ≥―–ΨΩΜζΙΙΥφΜζ≥ι»ΓΝΥ60ΟϊΗΏ÷–…ζΘ§Ά®ΙΐΈ ΨμΒς≤ιΘ§ΒΟΒΫ“‘œ¬ ΐΨίΘΚ
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

”…“‘…œ ΐΨίΘ§ΦΤΥψΒΟΒΫK2ΒΡΙέ≤β÷ΒkΓ÷9.643Θ§ΗυΨίΝΌΫγ÷Β±μΘ§“‘œ¬ΥΒΖ®’ΐ»ΖΒΡ «(ΓΓΓΓ)
A. ΟΜ”–≥δΉψΒΡάμ”…»œΈΣΩΈΆβ‘ΡΕΝΝΩ¥σ”κΉςΈΡ≥…Φ®”≈–ψ”–ΙΊ
B. ”–0.5%ΒΡΑ―Έ’»œΈΣΩΈΆβ‘ΡΕΝΝΩ¥σ”κΉςΈΡ≥…Φ®”≈–ψ”–ΙΊ
C. ”–99.9%ΒΡΑ―Έ’»œΈΣΩΈΆβ‘ΡΕΝΝΩ¥σ”κΉςΈΡ≥…Φ®”≈–ψ”–ΙΊ
D. ”–99.5%ΒΡΑ―Έ’»œΈΣΩΈΆβ‘ΡΕΝΝΩ¥σ”κΉςΈΡ≥…Φ®”≈–ψ”–ΙΊ