题目内容
已知函数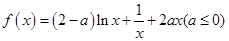 .
.
(1)当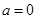 时,求
时,求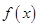 的极值;(2)当
的极值;(2)当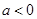 时,讨论
时,讨论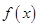 的单调性;
的单调性;
(3)若对任意的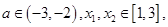 恒有
恒有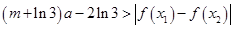 成立,求实数
成立,求实数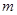 的取值范围.
的取值范围.
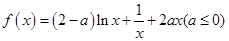 .
.(1)当
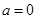 时,求
时,求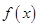 的极值;(2)当
的极值;(2)当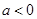 时,讨论
时,讨论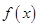 的单调性;
的单调性;(3)若对任意的
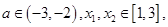 恒有
恒有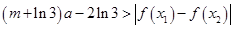 成立,求实数
成立,求实数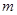 的取值范围.
的取值范围. (1)极小值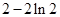 ,无极大值;(2)参考解析;(3)
,无极大值;(2)参考解析;(3)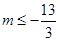
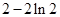 ,无极大值;(2)参考解析;(3)
,无极大值;(2)参考解析;(3)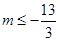
试题分析:(1)当
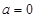 时.函数f(x)是一个对数函数和分式的和的形式.通过求导可以求出函数的有极小值,但没极大值.
时.函数f(x)是一个对数函数和分式的和的形式.通过求导可以求出函数的有极小值,但没极大值.(2)当
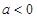 时.通过求导可得导函数的两个零点,在定义域
时.通过求导可得导函数的两个零点,在定义域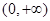 上分别对两个零点的大小讨论分类.从而得到函数的单调区间.
上分别对两个零点的大小讨论分类.从而得到函数的单调区间.(3)由对任意的
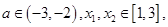 恒有
恒有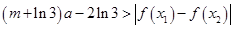 成立.首先要求出函数f(x)在[1,3]上且
成立.首先要求出函数f(x)在[1,3]上且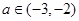 的最大值
的最大值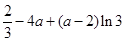 .从而对于任意
.从而对于任意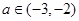 使得
使得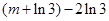
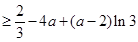 恒成立即可.再通过分离变量即可得到结论.本题前两小题较为基础但第二小题的分类做到清晰不容易,第三小题难度较大.
恒成立即可.再通过分离变量即可得到结论.本题前两小题较为基础但第二小题的分类做到清晰不容易,第三小题难度较大.试题解析:(1)当
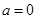 时,
时,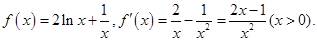 1分
1分由
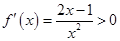 ,解得
,解得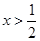 . 2分
. 2分∴
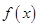 在
在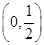 上是减函数,在
上是减函数,在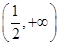 上是增函数. 3分
上是增函数. 3分∴
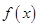 的极小值为
的极小值为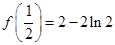 ,无极大值. 4分
,无极大值. 4分(2)
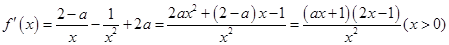 . 6分
. 6分①当
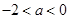 时,
时,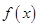 在
在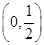 和
和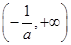 上是减函数,在
上是减函数,在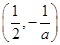 上是增函数; 7分
上是增函数; 7分②当
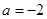 时,
时,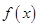 在
在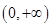 上是减函数; 8分
上是减函数; 8分③当
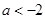 时,
时,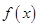 在
在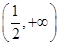 和
和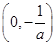 上是减函数,在
上是减函数,在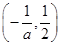 上是增函数. 9分
上是增函数. 9分(3)当
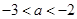 时,由(2)可知
时,由(2)可知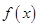 在
在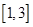 上是减函数,
上是减函数,∴
 . 10分
. 10分由
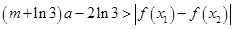 对任意的
对任意的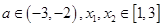 恒成立,
恒成立,∴
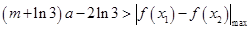 11分
11分即
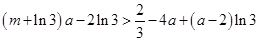 对任意
对任意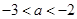 恒成立,
恒成立,即
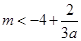 对任意
对任意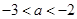 恒成立, 12分
恒成立, 12分由于当
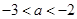 时,
时,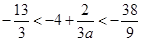 ,∴
,∴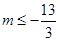 . 14分
. 14分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
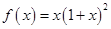 ,
,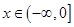 .
.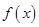 的极值点;
的极值点;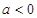 ,记
,记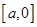 上的最小值为
上的最小值为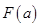 ,求
,求 的最小值.
的最小值.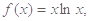
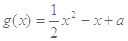 .
.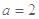 时,求
时,求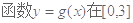 上的值域;
上的值域; 在
在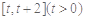 上的最小值;
上的最小值;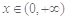 ,都有
,都有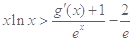 成立
成立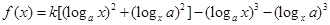 ,
, ,(其中
,(其中 ),设
),设 .
. 时,试将
时,试将 表示成
表示成 的函数
的函数 ,并探究函数
,并探究函数 时,若存在
时,若存在 ,使
,使 成立,试求
成立,试求 的范围.
的范围.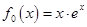 ,
,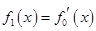 ,
,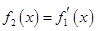 ,
,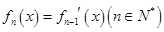 .
. 表达式(不需证明);
表达式(不需证明); ;
;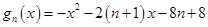 ,
,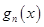 的最大值为
的最大值为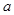 ,
,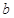 ,试求
,试求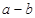 的最小值.
的最小值.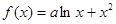 (
(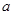 为实常数) .
为实常数) .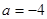 时,求函数
时,求函数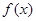 在
在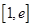 上的最大值及相应的
上的最大值及相应的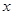 值;
值;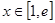 时,讨论方程
时,讨论方程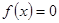 根的个数.
根的个数.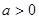 ,且对任意的
,且对任意的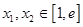 ,都有
,都有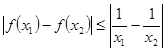 ,求实数a的取值范围.
,求实数a的取值范围.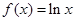 ,
,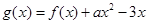 ,函数
,函数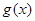 的图像在点
的图像在点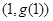 处的切线平行于
处的切线平行于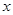 轴.
轴.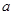 的值;
的值;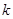 的直线与函数
的直线与函数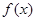 的图象交于两点
的图象交于两点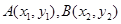 ,(
,(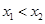 ),证明:
),证明: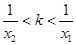 .
.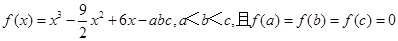 ,现给出如下结论:
,现给出如下结论: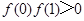 ;②
;②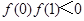 ;③
;③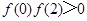 ;④
;④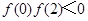 .
. (
( 为常实数)的定义域为
为常实数)的定义域为 ,关于函数
,关于函数 给出下列命题:
给出下列命题: ,存在正数
,存在正数 ,使得对于任意的
,使得对于任意的 ,都有
,都有 .
. 时,函数
时,函数 时,则
时,则 一定存在极值点;
一定存在极值点; 时,方程
时,方程 在区间(1,2)内有唯一解.
在区间(1,2)内有唯一解.