题目内容
4.在三棱锥S-ABC中,△ABC是边长为1的正三角形,SC⊥面ABC,SC=2,则三棱锥S-ABC外接球的表面积为( )| A. | 6π | B. | $\frac{16π}{3}$ | C. | $\frac{40π}{9}$ | D. | $\frac{8π}{3}$ |
分析 由已知结合三棱锥和正三棱柱的几何特征,可得此三棱锥外接球,即为以△ABC为底面以PA为高的正三棱柱的外接球,分别求出棱锥底面半径r,和球心距d,代入R=$\sqrt{{r}^{2}+{d}^{2}}$,可得球的半径R,然后求解表面积.
解答 解:根据已知中底面△ABC是边长为2的正三角形,SC⊥面ABC,SC=2,
可得此三棱锥外接球,即为以△ABC为底面以SC为高的正三棱柱的外接球,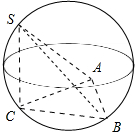
∵△ABC是边长为1的正三角形,
∴△ABC的外接圆半径r=$\frac{\sqrt{3}}{3}$,球心到△ABC的外接圆圆心的距离d=1,
故球的半径R=$\sqrt{{r}^{2}+{d}^{2}}$=$\sqrt{{(\frac{\sqrt{3}}{3})}^{2}+{1}^{2}}$=$\frac{2\sqrt{3}}{3}$.
三棱锥S-ABC外接球的表面积为:4π${×(\frac{2\sqrt{3}}{3})}^{2}$=$\frac{16π}{3}$.
故选:B.
点评 本题考查的知识点是球内接多面体,熟练掌握球的半径R公式R=$\sqrt{{r}^{2}+{d}^{2}}$,是解答的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
19.设全集U=R,集合A=$\{x|\frac{1}{16}≤{2^{-x}}$<1,x∈Z\},B={x|(x-3)(x+1)≥0,x∈Z},则(∁UB)∩A=( )
| A. | {0,1,2,3,4} | B. | {1,2,3} | C. | {0,1,2} | D. | {1,2} |
3.设H、P是△ABC所在平面上异于A、B、C的两点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{h}$分别表示向量$\overrightarrow{PA}$,$\overrightarrow{PB}$,$\overrightarrow{PC}$,$\overrightarrow{PH}$,已知$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{c}$•$\overrightarrow{h}$=$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{a}$•$\overrightarrow{h}$=$\overrightarrow{c}$•$\overrightarrow{a}$+$\overrightarrow{b}$•$\overrightarrow{h}$,$|{\overrightarrow{AH}}|=1$,$|{\overrightarrow{BH}}|=\sqrt{2}$,$|{\overrightarrow{BC}}|=\sqrt{3}$,点O是△ABC外接圆的圆心,则△AOB,△BOC,△AOC的面积之比为( )
| A. | $1:\sqrt{2}:\sqrt{3}$ | B. | $2:\sqrt{3}:1$ | C. | $1:\sqrt{3}:2$ | D. | $\sqrt{2}:1:\sqrt{3}$ |