题目内容
【题目】如图,正方形ABCD中边长为1,P、Q分别为BC、CD上的点,△CPQ周长为2. 
(1)求PQ的最小值;
(2)试探究求∠PAQ是否为定值,若是给出证明;不是说明理由.
【答案】
(1)解:设∠CPQ=θ,则CP=PQcosθ,CQ=PQsinθ
![]() (
( ![]() )
)
∴ ![]()
∴ ![]()
(2)解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,
设Q(x,1),P(1,y),设∠DAQ=α,∠PAB=β
∴ ![]() ,即xy+(x+y)=1
,即xy+(x+y)=1
又tanα=x,tanβ=y
∴ ![]() ,
,
∴ ![]()
∴ ![]()
【解析】(1)根据△CPQ周长为2,并且△CPQ是直角三角形,设∠CPQ=θ,根据三角函数的定义,CP=PQcosθ,CQ=PQsinθ,因此可以表示出 ![]() ,求该函数的最小值即可;(2)利用解析法求解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,设Q(x,1),P(1,y),利用两点间距离公式求出PQ,根据△CPQ周长为2,找出x,y的关系,求出∠PAQ的正切值,即可求得结果.
,求该函数的最小值即可;(2)利用解析法求解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,设Q(x,1),P(1,y),利用两点间距离公式求出PQ,根据△CPQ周长为2,找出x,y的关系,求出∠PAQ的正切值,即可求得结果.

 优等生题库系列答案
优等生题库系列答案【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
(Ⅰ)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望和方差.
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生
进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
88 | 83 | 117 | 92 | 108 | 100 | 112 | |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的理由;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到
是线性相关的,若该生的物理成绩达到![]() 分,请你估计他的数学成绩大约是多少?
分,请你估计他的数学成绩大约是多少?
(参考公式: 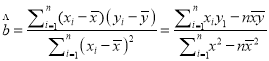 ,
, ![]() )
)
【题目】(12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作![]() 和
和![]() ,试求
,试求![]() 和
和![]() 的分布列和数学期望.
的分布列和数学期望.