题目内容
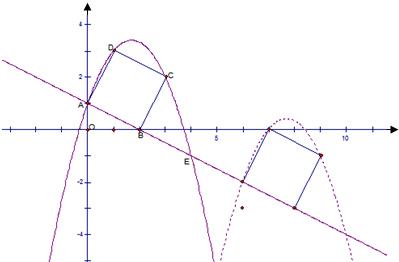 如图,直线y=-
如图,直线y=-| 1 |
| 2 |
(1)求抛物线的解析式.
(2)若正方形以每秒
| 5 |
分析:(1)可先根据AB所在直线的解析式求出A,B两点的坐标,即可得出OA、OB的长.过D作DM⊥y轴于M,则△ADM≌△BAO,由此可得出MD、MA的长,也就能求出D的坐标,同理可求出C的坐标;可根据A、C、D三点的坐标,用待定系数法求出抛物线的解析式;
(2)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当A′在x轴下方,但C′在x轴上方或x轴上时,即当1<t≤2时,S为梯形A′GB′H的面积,可参照①的方法求出A′G和B′H的长,那么梯形的上下底就可求出,梯形的高为A′B′即正方形的边长,可根据梯形的面积计算公式得出关于S、t的函数关系式.
③当D′逐渐移动到x轴的过程中,即当2<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
(2)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当A′在x轴下方,但C′在x轴上方或x轴上时,即当1<t≤2时,S为梯形A′GB′H的面积,可参照①的方法求出A′G和B′H的长,那么梯形的上下底就可求出,梯形的高为A′B′即正方形的边长,可根据梯形的面积计算公式得出关于S、t的函数关系式.
③当D′逐渐移动到x轴的过程中,即当2<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
解答:解:(1)(2)设抛物线为y=ax2+bx+c,抛物线过(0,1)(3,2)(1,3),
∴
解得
∴抛物线方程为y=-
x2+
x+1,.
(2)①当点A运动到点F时,t=1,
当0<t≤1时,
∵∠OFA=∠GFB′,
tan∠OFA=
=
,
∴tan∠GFB′=
=
=
,
∴GB′=
t
∴S△FB′G=
FB′×GB′
=
×
t×
=
t2;
②当点C运动到x轴上时,t=2,
当1<t≤2时,如图3,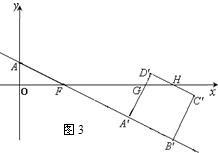
A′B′=AB=
=
,
∴A′F=
t-
,
∴A′G=
,
∵B′H=
,
∴S梯形A′B′HG=
(A′G+B′H)×A′B′
=
(
+
)×
=
t-
;
③当点D运动到x轴上时,t=3,
当2<t≤3时,如图4,
∵A′G=
,
∴GD′=
-
=
,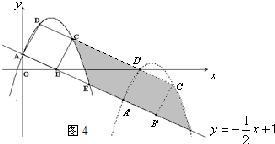
∵S△AOF=
×1×2=1,OA=1,△AOF∽△GD′H
∴
=(
)2,
∴S△GD′H=(
)2,
∴S五边形GA′B′C′H=(
)2-(
)2
=-
t2+
t-
;(1<t≤2)
∴
|
解得
|
∴抛物线方程为y=-
| 5 |
| 6 |
| 17 |
| 6 |
(2)①当点A运动到点F时,t=1,
当0<t≤1时,
∵∠OFA=∠GFB′,
tan∠OFA=
| OA |
| OF |
| 1 |
| 2 |
∴tan∠GFB′=
| GB′ |
| FB′ |
| GB′ | ||
|
| 1 |
| 2 |
∴GB′=
| ||
| 2 |
∴S△FB′G=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5 |
| 4 |
②当点C运动到x轴上时,t=2,
当1<t≤2时,如图3,

A′B′=AB=
| 22+12 |
| 5 |
∴A′F=
| 5 |
| 5 |
∴A′G=
| ||||
| 2 |
∵B′H=
| ||
| 2 |
∴S梯形A′B′HG=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 4 |
③当点D运动到x轴上时,t=3,
当2<t≤3时,如图4,
∵A′G=
| ||||
| 2 |
∴GD′=
| 5 |
| ||||
| 2 |
3
| ||||
| 2 |

∵S△AOF=
| 1 |
| 2 |
∴
| S△GD′H |
| S△AOF |
| GD′ |
| OA |
∴S△GD′H=(
3
| ||||
| 2 |
∴S五边形GA′B′C′H=(
| 5 |
3
| ||||
| 2 |
=-
| 5 |
| 4 |
| 15 |
| 2 |
| 25 |
| 4 |
点评:本题着重考查了待定系数法求二次函数解析式、图形平移变换、三角形相似等重要知识点,(3)小题中要根据正方形的不同位置分类进行讨论,不要漏解.

练习册系列答案
相关题目
 如图,直线
如图,直线 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: (2012•上海)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设:
(2012•上海)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设: