题目内容

已知函数f（x）= $数学公式$ 为奇函数，f（1）＜f（3），且不等式0≤f（x）≤ $数学公式$ 的解集为[-2，-1]∪[2，4]，则f（x）的解析式为________．

$\text{[math]}$
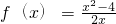
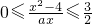分析：由函数f（x）是奇函数，可知f（-x）=-f（x），据此可解得b．由已知不等式0≤f（x）≤ $\text{[math]}$ 的解集为[-2，-1]∪[2，4]，及f（-2）=-f（2），可得f（2）=0，据此可算出c．再由f（1）＜f（3），得a＞0．由0≤f（x）≤ $\text{[math]}$ ，得 $\text{[math]}$ ，当x＞0时，其解集为[2，4]，可得a的值．
解答：∵函数f（x）是奇函数，∴f（-x）=-f（x），
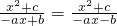∴ $\text{[math]}$ ，即-ax+b=-ax-b，即2b=0，
∴b=0．
由已知不等式0≤f（x）≤ $\text{[math]}$ 的解集为[-2，-1]∪[2，4]，
∴ $\text{[math]}$ ，
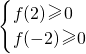又∵f（-2）=-f（2），
∴f（2）=0，即 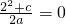$\text{[math]}$ ，即c+4=0，
∴c=-4．
∴可得f（x）= $\text{[math]}$ ．
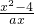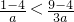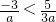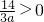由f（1）＜f（3），得 $\text{[math]}$ ，∴ $\text{[math]}$ ，∴ $\text{[math]}$ ，得a＞0．
由0≤f（x）≤ $\text{[math]}$ ，得 $\text{[math]}$ ，
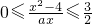当x＞0时，上不等式可化为 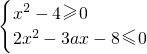$\text{[math]}$ ，可化为 $\text{[math]}$ ，
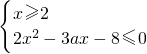∵当x＞0时，其解集为[2，4]，
∴4是方程2x²-3ax-8=0的解，
∴2×4²-3×4a-8=0，∴a=2．
可验证当a=2，b=0，c=-4时，满足题意．
故f（x）的解析式为f（x）= $\text{[math]}$ ．
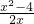故答案为f（x）= $\text{[math]}$ ．
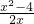点评：本题考查了函数的性质和不等式的解法，理解奇函数的性质和灵活的计算能力是解此题的关键．