题目内容
(本小题满分12分)
如图甲,直角梯形ABCD中,AB∥CD,,点M、N分别在AB、CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙)
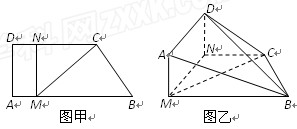
(1)求证:AB∥平面DNC;
(2)当DN的长为何值时,二面角D-BC-N的大小为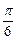 ?
?
如图甲,直角梯形ABCD中,AB∥CD,,点M、N分别在AB、CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙)

(1)求证:AB∥平面DNC;
(2)当DN的长为何值时,二面角D-BC-N的大小为
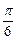 ?
?解:(1)∵MB∥NC,MB 平面DNC,NC
平面DNC,NC 平面DNC,
平面DNC,
∴MB∥平面DNC. …………2分
同理MA∥平面DNC,
又MA∩MB=M且MA、MB 平面MAB,
平面MAB,
∴平面MAB∥平面NCD, …………4分
又AB 平面MAB,
平面MAB,
∴AB∥平面NCD. …………5分
(2)过N作NH⊥BC交BC延长线于H,连结DH, …………6分
∵平面AMND⊥平面MNCB,DN⊥MN
∴DN⊥平面MNCB,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角。 …………8分
由BC=2,MB=4,MC⊥CB,知 ,
,
∴ …………10分
…………10分
由条件知: ,
,
∴ …………12分
…………12分
 平面DNC,NC
平面DNC,NC 平面DNC,
平面DNC,∴MB∥平面DNC. …………2分
同理MA∥平面DNC,
又MA∩MB=M且MA、MB
 平面MAB,
平面MAB,∴平面MAB∥平面NCD, …………4分
又AB
 平面MAB,
平面MAB,∴AB∥平面NCD. …………5分
(2)过N作NH⊥BC交BC延长线于H,连结DH, …………6分
∵平面AMND⊥平面MNCB,DN⊥MN
∴DN⊥平面MNCB,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角。 …………8分
由BC=2,MB=4,MC⊥CB,知
 ,
,
∴
 …………10分
…………10分由条件知:
 ,
,∴
 …………12分
…………12分略

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 ,
,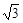 ,
, ,这个长方体的对角线长是
,这个长方体的对角线长是 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面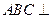 平面
平面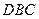 ,过点
,过点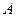 作
作 平面
平面 ,且
,且 .
.
 平面
平面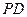 与平面
与平面 分10分)
分10分) B1C1D1中,AA1 =
B1C1D1中,AA1 =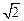 ,AB = 1,E是DD1的中点.
,AB = 1,E是DD1的中点.
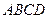 所在平面与圆
所在平面与圆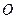 所在平面相交于
所在平面相交于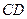 ,线段
,线段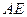 垂直于圆
垂直于圆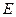 是圆
是圆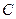 、
、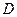 的点,
的点,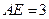 ,圆
,圆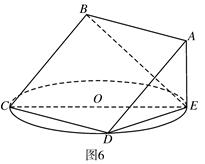
 平面
平面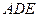 ;
;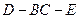 的平面角的正切值。
的平面角的正切值。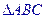 中
中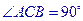 ,
,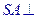 面
面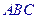 ,
,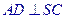 ,求证:
,求证: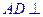 面
面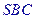 .
.
 ,若侧棱
,若侧棱 ,则正三棱锥S—ABC外接球的表面积是()
,则正三棱锥S—ABC外接球的表面积是()

 .36
.36
 ,则原图形的面积为( )
,则原图形的面积为( ) 

 4
4