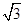题目内容
已知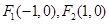 是椭圆的两个焦点,过
是椭圆的两个焦点,过 的直线
的直线 交椭圆于
交椭圆于 两点,若
两点,若 的周长为
的周长为 ,则椭圆方程为( )
,则椭圆方程为( )
A. | B.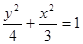 |
C. | D.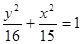 |
A
解析试题分析:∵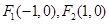 是椭圆的两个焦点∴c=1,又根据椭圆的定义,
是椭圆的两个焦点∴c=1,又根据椭圆的定义, 的周长=4a=8,得a=2,进而得b=
的周长=4a=8,得a=2,进而得b=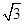 ,所以椭圆方程为
,所以椭圆方程为 .
.
考点:椭圆的定义和标准方程.

练习册系列答案
相关题目
抛物线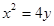 的焦点坐标是( )
的焦点坐标是( )
| A.(2,0) | B.(0,2) | C.(l,0) | D.(0,1) |
若θ是任意实数,则方程x2+4y2 =1所表示的曲线一定不是 ( )
=1所表示的曲线一定不是 ( )
| A.圆 | B.双曲线 | C.直线 | D.抛物线 |
椭圆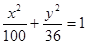 的焦距等于( )
的焦距等于( )
| A.20 | B.16 | C.12 | D.8 |
已知 两点,过动点
两点,过动点 作
作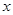 轴的垂线,垂足为
轴的垂线,垂足为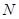 ,若
,若 ,当
,当 时,动点
时,动点 的轨迹为( )
的轨迹为( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
若双曲线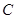 :
: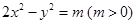 与抛物线
与抛物线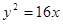 的准线交于
的准线交于 两点,且
两点,且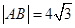 ,则
,则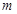 的值是( )
的值是( )
A.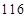 | B.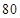 | C. | D.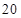 |
已知直线l交椭圆4x2+5y2=80于M,N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是 ( ).
| A.6x-5y-28=0 | B.6x+5y-28=0 |
| C.5x+6y-28=0 | D.5x-6y-28=0 |
 、
、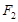 是双曲线
是双曲线
 ,
, 的左、右焦点,过
的左、右焦点,过 与双曲线的左、右两个分支分别交于点
与双曲线的左、右两个分支分别交于点 、
、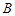 ,若
,若 为等边三角形,则该双曲线的离心率为 ( )
为等边三角形,则该双曲线的离心率为 ( )


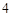

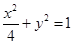 ,
, 为坐标原点.若
为坐标原点.若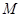 为椭圆上一点,且在
为椭圆上一点,且在 轴右侧,
轴右侧, 为
为 轴上一点,
轴上一点, ,则点
,则点