题目内容
 (本题满分14分)
(本题满分14分)
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
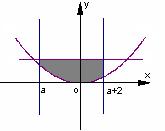
(3)设轨迹E与直线![]() 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
(1) x2=4y(x≠0,x≠![]() ) (3)
) (3) ![]()
解析:
(1) 解法1:依题意知,CD⊥AD,且|CD|=|BC|.依抛物线的定义可知点C的轨迹是以B为焦点,以AD为准线的抛物线除去顶点和与直线y=1的交点。---2分∵|OB|=1 ∴C的轨迹E的方程为x2=4y(x≠0,x≠![]() )--4分
)--4分
解法2:设C(x,y)则|CD|=y+1,|CB|=![]()
![]() ,
,
又|CD|=|BC|. ![]() ,化简得:x2=4y(x≠0,x≠
,化简得:x2=4y(x≠0,x≠![]() )
)
(2)解法1:设P(x,y)是轨迹E上一点,则P到直线y=x-2的距离
![]()
当x=2时,d取得最小值![]() ,这时x=2,y=1, ---------------------7分
,这时x=2,y=1, ---------------------7分
即点P(2,1).但由(Ⅰ)知点(2,1)不在轨迹E上,∴在轨迹E上这样的点P不存在。--8分
解法2:所求点即与直线y=x-2平行的轨迹E的切线与E的切点,
由![]() 得
得![]() ,
, ![]() ,∴
,∴![]() ,
,
下同解法1。
解法3:设与直线y=x-2 平行,与抛物线E相切的直线为
x-y+m=0,由方程组
![]()
![]() 有一解得方程
有一解得方程 ![]() 有两个相等的实根
有两个相等的实根
∴ ![]() ∴m=-1从而得方程组的解为
∴m=-1从而得方程组的解为![]() ,下同上.
,下同上.
(3) ∵-2<a<0 ∴ 0<a+2<2
根据图形结合定积分的几何意义可得:
![]() ----------------------------11分
----------------------------11分
![]()
![]()
![]() ----------------------------13分
----------------------------13分
当![]() 时,
时,![]() ------------- --------------14分
------------- --------------14分

 阅读快车系列答案
阅读快车系列答案 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).