题目内容
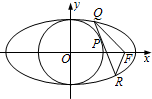
已知椭圆
C:+y2=1(a>1)的右焦点为F(c,0)(c>1),点P在圆O:x
2+y
2=1上任意一点(点P第一象限内),过点P作圆O的切线交椭圆C于两点Q、R.
(1)证明:|PQ|+|FQ|=a;
(2)若椭圆离心率为
,求线段QR长度的最大值.
分析:(1)设Q(x
1,y
1)(x
1>0),先求得|FQ|;再利用PQ是圆x
2+y
2=1的切线,求出|PQ|,即可证得结论;
(2)利用椭圆离心率为
,可求得a.
方法一:设直线QR的方程为y=kx+m,利用直线QR与圆O相切,可得m
2=k
2+1,将直线方程代入椭圆方程,从而可求|QR|,再利用基本不等式,即可求得结论;
方法二:设P(x
0,y
0),Q(x
1,y
1),R(x
2,y
2),则直线QR的方程为x
0x+y
0y=1,与椭圆方程联立,从而可求|QR|,再利用基本不等式,即可求得结论.
解答:(1)证明:设Q(x
1,y
1)(x
1>0),得|FQ|=a-ex
1,…(3分)
∵PQ是圆x
2+y
2=1的切线,∴
|PQ|==,
∵
+y12=1,∴
|PQ|===ex1,…(6分)
所以|PQ|+|FQ|=a. …(7分)
(2)解:由题意,
e==,∴a=2. …(9分)
方法一:设直线QR的方程为y=kx+m,∵点P在第一象限,∴k<0,m>0.
由直线QR与圆O相切,∴
=1,∴m
2=k
2+1. …(11分)
由
,消y得(1+4k
2)x
2+8kmx+4m
2-4=0,
设R(x
1,y
1),Q(x
2,y
2),则
x1+x2=-.
由(1)知,
|QR|=e(x1+x2)=(-)=4•=4•,…(14分)
∵
m2+3k2≥2m|k|,∴
|QR|≤4•=2.
当且仅当
m=-k时,|QR|取最大值2,此时直线QR的方程为
y=k(x-),过焦点F.…(16分)
方法二:设P(x
0,y
0),Q(x
1,y
1),R(x
2,y
2),则直线QR的方程为x
0x+y
0y=1. …(11分)
由
,消y得
(+4)x2-8x0x+4-4=0,则
x1+x2=,
∵
+=1,∴
x1+x2=,
由(1)知,
|QR|=e(x1+x2)=•=4•=4•,…(14分)
∵
+3x0≥2,∴
|QR|≤4•=2,
当且仅当
x0=时,|QR|取最大值2,此时
P(,),直线QR过焦点F. …(16分)
点评:本题考查椭圆的定义,考查直线与圆、椭圆的位置关系,考查基本不等式的运用,正确表示|QR|是关键.
练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: