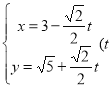题目内容
【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为![]() ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
【答案】(1)![]() (2)他们都选择方案乙进行抽奖时,累计得分的数学期望较大.
(2)他们都选择方案乙进行抽奖时,累计得分的数学期望较大.
【解析】
试题分析:(1)累计得分不小于3分的事件包含两种情况,一是小明中奖,小红不中奖;二是小明中奖,小红中奖,先根据独立事件同时发生概率的乘积公式得两种情况的概率,再根据互斥事件概率和的公式求概率(2)根据两种方案的数学期望值的大小确定方案好差,先确定两种方案的随机变量取法,再分别求对应概率,列表的分布列,最后根据数学期望公式求数学期望
试题解析:(1)由已知得,小明中奖的概率为![]() ,小红中奖的概率为
,小红中奖的概率为![]() ,且两人中奖与否互不影响,记“这2人的累计得分
,且两人中奖与否互不影响,记“这2人的累计得分![]() ” 的事件为
” 的事件为![]() ,则事件
,则事件![]() 包含有“
包含有“![]() ”,“
”,“ ![]() ”,2个两两互斥的事件,因为,
”,2个两两互斥的事件,因为,
![]()
(2)设小明、小红都选择方案甲所获得的累计得分为![]() ,都选择方案乙所获得的累计得分为
,都选择方案乙所获得的累计得分为![]() ,则
,则![]() 、
、![]() 的分布列如下:
的分布列如下:
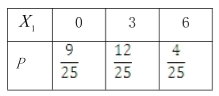
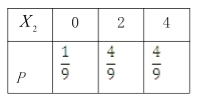
所以![]() ,
,
![]()
![]()
所以他们都选择方案乙进行抽奖时,累计得分的数学期望较大.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目