题目内容
设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
 ∪
∪
由已知得 =4,
=4, =1,e1·e2=2×1×cos60°=1.
=1,e1·e2=2×1×cos60°=1.
∴(2te1+7e2)·(e1+te2)=2t +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t =2t2+15t+7.欲使夹角为钝角,需2t2+15t+7<0,得-7<t<-
=2t2+15t+7.欲使夹角为钝角,需2t2+15t+7<0,得-7<t<- .
.
设2te1+7e2=λ(e1+te2)(λ<0),
∴ ,∴2t2=7,
,∴2t2=7,
∴t=- ,此时λ=-
,此时λ=- .
.
即t=- 时,向量2te1+7e2与e1+te2的夹角为π.
时,向量2te1+7e2与e1+te2的夹角为π.
∴夹角为钝角时,t的取值范围是 ∪
∪
 =4,
=4, =1,e1·e2=2×1×cos60°=1.
=1,e1·e2=2×1×cos60°=1.∴(2te1+7e2)·(e1+te2)=2t
 +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t =2t2+15t+7.欲使夹角为钝角,需2t2+15t+7<0,得-7<t<-
=2t2+15t+7.欲使夹角为钝角,需2t2+15t+7<0,得-7<t<- .
.设2te1+7e2=λ(e1+te2)(λ<0),
∴
 ,∴2t2=7,
,∴2t2=7,∴t=-
 ,此时λ=-
,此时λ=- .
.即t=-
 时,向量2te1+7e2与e1+te2的夹角为π.
时,向量2te1+7e2与e1+te2的夹角为π.∴夹角为钝角时,t的取值范围是
 ∪
∪

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
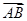 -t
-t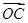 )·
)·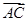 =(1,2),
=(1,2), =(-4,2),则该四边形的面积为( )
=(-4,2),则该四边形的面积为( )
 共线的单位向量是
共线的单位向量是 ;
; 的最小正周期为
的最小正周期为 ;
; 是偶函数;
是偶函数; 是
是 所在平面内一点,若
所在平面内一点,若 ,则
,则 的值域为
的值域为 ,则
,则 的取值范围是
的取值范围是 .
. 是平面内两个非零向量,则平面内任一向量
是平面内两个非零向量,则平面内任一向量 都可表示为
都可表示为 ,其中
,其中 ;
; ;
; 的一个方向向量为
的一个方向向量为 ;
; 与
与 夹角为
夹角为 ,且
,且 ,则|
,则| ;
; 是(
是(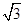 ,-1),则|a-b|的最大值为( )
,-1),则|a-b|的最大值为( )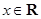 ,向量
,向量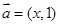 ,
,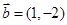 ,且
,且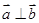 ,则
,则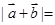 .
. ,
, 若
若 ,则
,则 _____________.
_____________.