题目内容
(2008•佛山二模)A是满足不等式组
的区域,B是满足不等式组
的区域,区域A内的点P的坐标为(x,y),
(Ⅰ)当x,y∈R时,求P∈B的概率;
(Ⅱ)当x,y∈Z时,求P∈B的概率.
|
|
(Ⅰ)当x,y∈R时,求P∈B的概率;
(Ⅱ)当x,y∈Z时,求P∈B的概率.
分析:(I)由题意可得是与面积有关的几何概率的求解,利用线性规划的知识,分别画出不等式组所表示的平面区域,分别计算面积,代入几何概率公式可求.
(II)因为x,y∈Z,且
,基本事件是有限的,所以为古典概型,这样求得总的基本事件的个数,再求得满足x,y∈Z,且
的基本事件的个数,然后求比值即为所求的概率.
(II)因为x,y∈Z,且
|
|
解答: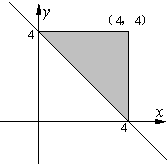 解:画出不等式组
解:画出不等式组
表示的可行域如图所示,
其中D(4,0),E(4,4),F(0,4)…(2分)B为图中阴影部分…(3分)
(Ⅰ)当x,y∈R时,事件“P∈B”的概率为
=
…(7分)
(Ⅱ)当x,y∈Z时,A中含整点个数N=5×5=25,B中含整点个数N0=15…(10分)
从而事件“P∈B”的概率为
=
=
答:当x,y∈R时,P∈B”的概率为
;当x,y∈Z时,P∈B的概率为
.
…(12分)
 解:画出不等式组
解:画出不等式组
|
其中D(4,0),E(4,4),F(0,4)…(2分)B为图中阴影部分…(3分)
(Ⅰ)当x,y∈R时,事件“P∈B”的概率为
| S△DEF |
| S正方形ODEF |
| 1 |
| 2 |
(Ⅱ)当x,y∈Z时,A中含整点个数N=5×5=25,B中含整点个数N0=15…(10分)
从而事件“P∈B”的概率为
| N0 |
| N |
| 15 |
| 25 |
| 3 |
| 5 |
答:当x,y∈R时,P∈B”的概率为
| 1 |
| 2 |
| 3 |
| 5 |
…(12分)
点评:本题主要考查几何概型中的面积类型和古典概型,两者最明显的区别是古典概型的基本事件是有限的,几何概型的基本事件是无限的.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目