题目内容

（2008•佛山二模）已知A为xOy平面内的一个区域．
命题甲：点(a，b)∈{(x，y)|
0≤x≤π
0≤y≤sinx
；命题乙：点（a，b）∈A．如果甲是乙的充分条件，那么区域A的面积的最小值是（　　）
分析：先利用图象作出命题甲对应的平面区域B，然后利用甲是乙的充分条件，确定平面区域A与B之间的面积关系．
解答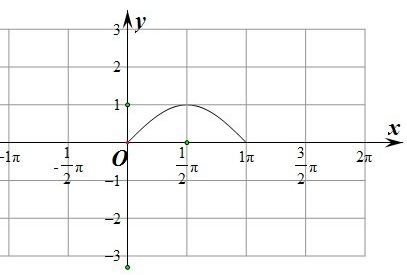：解：先作出命题甲对应的平面区域，如图：
则由积分可求区域面积为∫
 
π
0
sinxdx=-cosx
|
π
0
=2．
要使甲是乙的充分条件，则区域A的面积的最小值是2．
故选B．
点评：本题的考点是利用充分条件去判断两个命题之间的关系．在求解命题甲时，要用到定积分的有关知识，本题综合性较强．
练习册系列答案
相关题目
（2008•佛山二模）函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜
π
2
)的图象上一个最高点的坐标为(
π
12
，3)，与之相邻的一个最低点的坐标为(
7π
12
，-1)．
（Ⅰ）求f（x）的表达式；
（Ⅱ）求f（x）在x=
π
6
处的切线方程．
（2008•佛山二模）已知函数f（x）的自变量的取值区间为A，若其值域区间也为A，则称A为f（x）的保值区间．
（1）求函数f（x）=x2形如[n，+∞）（n∈R）的保值区间；
（2）函数g(x)=|1-
1x
|(x＞0)是否存在形如[a，b]（a＜b）的保值区间？若存在，求出实数a，b的值，若不存在，请说明理由．
（2008•佛山二模）已知正项等差数列{an}的前n项和为Sn，其中a1≠a2，am、ak、ah都是数列{an}中满足ah-ak=ak-am的任意项．
（Ⅰ）证明：m+h=2k；
（Ⅱ）证明：Sm•Sh≤Sk2；
（III）若
Sm
、
Sk
、
Sh
也成等差数列，且a1=2，求数列{
1
Sn-S1
}(n∈N*，n≥3)的前n项和Tn＜
5
24
．
（2008•佛山二模）在△ABC中，若
AC
•
BC
=1，
AB
•
BC
=-2，则|
BC
|=
3
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网