题目内容
【题目】已知函数
.
（1）若函数f(x)在定义域内是增函数，求实数a的取值范围；
（2）当a∈[1，e)时，求方程
的根的个数.
【答案】（1）
（2）有且只有一个根
【解析】
（1）
，即
，求函数
的最大值得到答案.
（2）求导
，讨论
，
两种情况，根据单调性得到
的极大值为
，设
，求导得到函数单调递增，再根据零点存在定理得到答案.
（1）定义域：
，在
时恒成立，
即
在时恒成立，所以时，，
由于
，所以.
（2）设
=
，
①当时，
，在
是单调递增，
，
，
所以存在唯一的
使
，即方程
只有一个根.
②当时，则
，令
，有
或
.
所以在
上是增函数，在
上是减函数，在
上是增函数，
的极大值为
.
设，其中，则
.
所以
在上是增函数，所以
，即
，
所以
在
上无零点.
又
，
，所以
，
又
在
单调递增，所以存在唯一的使.
即方程只有一个根.
综上所述，当
时，方程有且只有一个根.
【题目】某校高三（1）班在一次语文测试结束后，发现同学们在背诵内容方面失分较为严重.为了提升背诵效果，班主任倡议大家在早、晚读时间站起来大声诵读，为了解同学们对站起来大声诵读的态度，对全班50名同学进行调查，将调查结果进行整理后制成下表：
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
（1）欲使测试优秀率为30%，则优秀分数线应定为多少分？
（2）依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系，列出2×2列联表，并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据：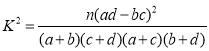
，
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某公司为评估两套促销活动方案（方案1运作费用为5元/件；方案2的运作费用为2元件），在某地区部分营销网点进行试点（每个试点网点只采用一种促销活动方案），运作一年后，对比该地区上一年度的销售情况，制作相应的等高条形图如图所示.
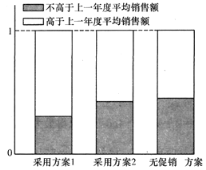
（1）请根据等高条形图提供的信息，为该公司今年选择一套较为有利的促销活动方案（不必说明理由）；
（2）已知该公司产品的成本为10元/件（未包括促销活动运作费用），为制定本年度该地区的产品销售价格，统计上一年度的8组售价
（单位：元/件，整数）和销量
（单位：件）
如下表所示：
售价 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
销量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①请根据下列数据计算相应的相关指数
，并根据计算结果，选择合适的回归模型进行拟合；
②根据所选回归模型，分析售价
定为多少时？利润
可以达到最大.
|
|
| |
| 52446.95 | 13142 | 122.89 |
| 124650 | ||
（附：相关指数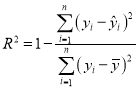
）
