题目内容
关于x的方程(x2-1)2-|x2-1|+k=0,给出下列四个命题:①存在实数k,使得方程恰有2个不同的实根;
②存在实数k,使得方程恰有4个不同的实根;
③存在实数k,使得方程恰有5个不同的实根;
④存在实数k,使得方程恰有8个不同的实根.
其中假命题的个数是( )
A.0 B.1 C.2 D.3
解析:令t=x2-1,且y=t2-|t|,y=-k,在同一坐标系中作出函数y=t2-|t|,y=-k的图像,如图所示.
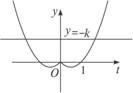
当k=0时,函数y=t2-|t|,y=-k的图像有3个交点,-1,0,1,相应地,应有x2-1=1,x2-1=-1,x2-1=0,则此时方程有5个根;
当k<0时,此时-k>0,函数y=t2-|t|,y=-k的图像有2个交点,此时t2-|t|+k=0,Δ=1-4k>0,从而|t|=![]() ,即x2=
,即x2=![]() ,或x2=
,或x2=![]() <0(舍去),则此时方程有2个不同的根;
<0(舍去),则此时方程有2个不同的根;
当k=![]() 时,函数y=t2-|t|,y=-k的图像有2个交点,且|x2-1|=
时,函数y=t2-|t|,y=-k的图像有2个交点,且|x2-1|=![]() ,则此时方程有4个根;
,则此时方程有4个根;
当0<k<![]() 时,函数y=t2-|t|,y=-k的图像有4个交点,从而原方程有8个根.
时,函数y=t2-|t|,y=-k的图像有4个交点,从而原方程有8个根.
从而假命题的个数为0,故选A.
答案:A

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目