题目内容
(本小题满分12分)已知数列满足a 1=1,an+1=2an+1(n∈N*)
1=1,an+1=2an+1(n∈N*)
(1) 求证:数列 {an+1}是等比数列;
{an+1}是等比数列;
(2) 求{an}的通项公式.
 1=1,an+1=2an+1(n∈N*)
1=1,an+1=2an+1(n∈N*)(1) 求证:数列
 {an+1}是等比数列;
{an+1}是等比数列;(2) 求{an}的通项公式.
证明: 由an+1=2an+1得an+1+1=2(an+1)
又an+1≠0 ∴
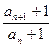 =2
=2即{an+1}为等比数列.--------------------7
(2)解析: 由(1)知an+1=(a1+1)qn-1
即an=(a1+1)qn-1-1=2·2n-1-1=2n-1 -------------5
略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
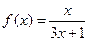 ,数列
,数列 满足
满足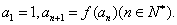
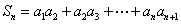 ,求
,求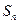 .
.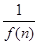 ,bn=f(
,bn=f(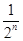 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<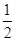 .
.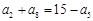 ,则S9等于( )
,则S9等于( )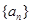 的前
的前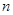 项和为
项和为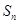 ,且
,且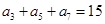 ,则
,则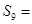 ( )
( )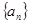 的前
的前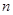 项和为
项和为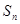 ,
,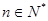 ,且
,且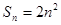 ,则
,则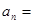
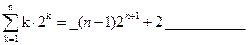
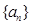 的前n项和为
的前n项和为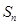 ,
,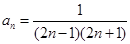 且
且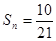 ,则n=( )
,则n=( )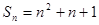 ,则
,则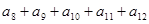 =___________.
=___________.