题目内容
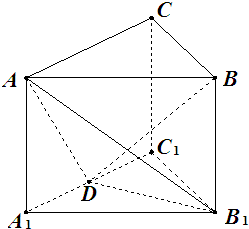（2007•盐城一模）如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=2，BC=BB1=1，D是棱A1C1的中点．（1）设平面BB1D与棱AC交于点E，确定点E的位置并给出理由；
（2）求直线AB与平面BB1D所成角的大小；
（3）求二面角B-AD-B1的大小．
分析：（1）证明：E是AC的中点．由题意可得：B1B∥平面A1CC1A，再根据线面平行的性质定理可得：DE∥B1B，即可得到DE∥A1A，进而得到答案．
（2）由几何体的结构得：平面BB1DE⊥底面ABC．过A点作AM⊥BE，M是垂足，M在BE的延长线上，可得AM⊥平面BB1DF，所以∠ABM就是直线AB与平面BDB1所成角，再利用解三角形的知识求出答案即可（3）根据线段的长度关系可得：AB2=AD2+BD2，即AD⊥DB．在△ADB1中，由余弦定理可得：∠ADB1=1200，所以∠DAB1=∠DB1A=30°．过点D作DP⊥AD，垂足为P，则∠PDB是二面角B-AD-B1的平面角，再利用解三角形的有关知识求出二面角的平面角即可．
（2）由几何体的结构得：平面BB1DE⊥底面ABC．过A点作AM⊥BE，M是垂足，M在BE的延长线上，可得AM⊥平面BB1DF，所以∠ABM就是直线AB与平面BDB1所成角，再利用解三角形的知识求出答案即可（3）根据线段的长度关系可得：AB2=AD2+BD2，即AD⊥DB．在△ADB1中，由余弦定理可得：∠ADB1=1200，所以∠DAB1=∠DB1A=30°．过点D作DP⊥AD，垂足为P，则∠PDB是二面角B-AD-B1的平面角，再利用解三角形的有关知识求出二面角的平面角即可．
解答：解：（1）证明：E是AC的中点． …（1分）
由棱柱的性质知B1B∥平面A1CC1A，
∵AB⊆平面ABD，平面A1CC1A∩平面BB1D=DE，
∴所以DE∥B1B，
∴DE∥A1A，
因为D是A1C1的中点，
所以E是AC中点．…（4分）
（2）∵BB1⊥底面，
∴平面BB1DE⊥底面ABC．
过A点作AM⊥BE，M是垂足，M在BE的延长线上，
∴AM⊥平面BB1DF
所以，∠ABM就是直线AB与平面BDB1所成角．…（6分）
在直角△ACB中，AB=
，又因为∠BEC=∠AEM=45°，
所以AM=
，
∴sin∠ABM=
=
，∠ABM=arcsin
． …（8分）
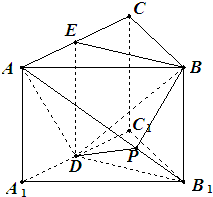（3）如图，由题意可得：在直角AA1D中AD=
，在直角△BB1D中BD=
，在直角△ACB中AB=
，
∴AB2=AD2+BD2，
∴AD⊥DB．
在△ADB1中，AD=DB1=
，AB1=
，
∴由余弦定理可得：∠ADB1=1200，所以∠DAB1=∠DB1A=30°．
过点D作DP⊥AD，垂足为P，则∠PDB是二面角B-AD-B1的平面角． …（11分）
连接BP，所以在等腰△ADB1中DP=
，B1P=
，在直角△ABB1中，BP=1，
所以在△PDB中，由余弦定理可得：cos∠PDB=
=
=
，
∴二面角B-AD-B1的大小为arccos
． …（14分）
由棱柱的性质知B1B∥平面A1CC1A，
∵AB⊆平面ABD，平面A1CC1A∩平面BB1D=DE，
∴所以DE∥B1B，
∴DE∥A1A，
因为D是A1C1的中点，
所以E是AC中点．…（4分）
（2）∵BB1⊥底面，
∴平面BB1DE⊥底面ABC．
过A点作AM⊥BE，M是垂足，M在BE的延长线上，
∴AM⊥平面BB1DF
所以，∠ABM就是直线AB与平面BDB1所成角．…（6分）
在直角△ACB中，AB=
| 5 |
所以AM=
| ||
| 2 |
∴sin∠ABM=
| ||||
|
| ||
| 10 |
| ||
| 10 |
（3）如图，由题意可得：在直角AA1D中AD=| 2 |
| 3 |
| 5 |
∴AB2=AD2+BD2，
∴AD⊥DB．
在△ADB1中，AD=DB1=
| 2 |
| 6 |
∴由余弦定理可得：∠ADB1=1200，所以∠DAB1=∠DB1A=30°．
过点D作DP⊥AD，垂足为P，则∠PDB是二面角B-AD-B1的平面角． …（11分）
连接BP，所以在等腰△ADB1中DP=
| ||
| 3 |
| ||
| 3 |
所以在△PDB中，由余弦定理可得：cos∠PDB=
| DP2+DB2-PB2 |
| 2DP•DB |
(
| ||||||
2×
|
2
| ||
| 3 |
∴二面角B-AD-B1的大小为arccos
2
| ||
| 3 |
点评：解决此类问题的关键是熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，结合有关定理进行证明即可，并且也有利于建立空间之间坐标系，利用向量的有关知识解决空间角与空间距离等问题．
练习册系列答案
相关题目