题目内容
已知动点M与F（1，0）的距离比它到直线l：x+3=0的距离小2，设M的轨迹为G，正项数列{an}满足a1=2，且（an，
）在曲线G上，则数列{an}的通项公式为（ ）
| 2an+1 |
| A、an=2n |
| B、an=2n-1 |
| C、an=2n+1 |
| D、an=2-1 |
考点：轨迹方程
专题：综合题,等差数列与等比数列,圆锥曲线的定义、性质与方程
分析：先利用抛物线的定义，可得M的轨迹为抛物线，方程为y2=4x，利用（an，
）在曲线G上，可得an+1=2an，
进而可求数列{an}的通项公式．
| 2an+1 |
进而可求数列{an}的通项公式．
解答：
解：∵动点M与F（1，0）的距离比它到直线l：x+3=0的距离小2，
∴动点M与F（1，0）的距离等于它到直线l：x=-1的距离，
∴M的轨迹为抛物线，方程为y2=4x．
∵（an，
）在曲线G上，
∴an+1=2an，
∵正项数列{an}满足a1=2，
∴数列{an}是以2为首项，2为公比的等比数列，
∴an=2n．
故选：A．
∴动点M与F（1，0）的距离等于它到直线l：x=-1的距离，
∴M的轨迹为抛物线，方程为y2=4x．
∵（an，
| 2an+1 |
∴an+1=2an，
∵正项数列{an}满足a1=2，
∴数列{an}是以2为首项，2为公比的等比数列，
∴an=2n．
故选：A．
点评：本题考查抛物线的定义，考查等比数列的定义域通项，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
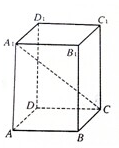如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，高A1A=3，体积为24，则对角线A1C为
函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜