题目内容
数列{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,且a1+3,3a2,a3+4成等差数列.
(1)求数列{an}的通项公式;
(2)令数列{bn}满足bn=lna3n+1,记数列{bn}的前n项和为Tn,求:
+
+…+
.
(1)求数列{an}的通项公式;
(2)令数列{bn}满足bn=lna3n+1,记数列{bn}的前n项和为Tn,求:
| ln2 |
| T1 |
| ln2 |
| T2 |
| ln2 |
| Tn |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)首先根据条件建立关系式,进一步求出数列的通项公式.
(2)根据(1)的结论求出相关的通项公式,进一步利用裂项相消法求数列的和.
(2)根据(1)的结论求出相关的通项公式,进一步利用裂项相消法求数列的和.
解答:
解:Sn为数列{an}的前n项和,已知S3=7,且a1+3,3a2,a3+4成等差数列.
则:
解得:a2=2
设等比数列的公比为q
则:
+2+2q=7
解得:q=2或
由于q>1
故q=2
所以:an=2n-1
(2)令数列{bn}满足bn=lna3n+1,
bn=ln23n=3nln2
由于bn+1-bn=3ln2
所以{bn}是等差数列.
记数列{bn}的前n项和为Tn=
=
所以:
=
=
(
-
)
Sn=
+
+…+
=
(1-
+
-
+…+
-
)=
则:
|
解得:a2=2
设等比数列的公比为q
则:
| 2 |
| q |
解得:q=2或
| 1 |
| 2 |
由于q>1
故q=2
所以:an=2n-1
(2)令数列{bn}满足bn=lna3n+1,
bn=ln23n=3nln2
由于bn+1-bn=3ln2
所以{bn}是等差数列.
记数列{bn}的前n项和为Tn=
| n(b1+bn) |
| 2 |
| 3n(n+1)ln2 |
| 2 |
所以:
| ln2 |
| Tn |
| ln2 | ||
|
| 2 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
Sn=
| ln2 |
| T1 |
| ln2 |
| T2 |
| ln2 |
| Tn |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2n |
| 3n+3 |
点评:本题考查的知识要点:数列通项公式的求法,数列的求和.属于基础题型

练习册系列答案
相关题目
已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别与抛物线交于点C,D设直线AB,CD的斜率分别为k1,k2,则
等于( )
| k1 |
| k2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知动点M与F(1,0)的距离比它到直线l:x+3=0的距离小2,设M的轨迹为G,正项数列{an}满足a1=2,且(an,
)在曲线G上,则数列{an}的通项公式为( )
| 2an+1 |
| A、an=2n |
| B、an=2n-1 |
| C、an=2n+1 |
| D、an=2-1 |
若把函数 y=sin(x+
)的图象向右平移m(m>0)个单位长度后,得到y=sinx的图象,则m的最小值( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
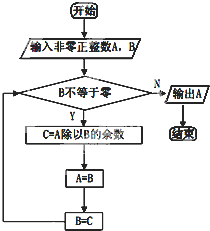 在如图的算法中,如果输入A=138,B=22,则输出的结果是( )
在如图的算法中,如果输入A=138,B=22,则输出的结果是( )| A、2 | B、4 | C、128 | D、0 |
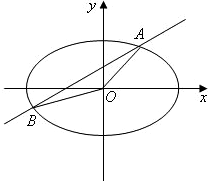 如图,直线y=x+b与椭圆
如图,直线y=x+b与椭圆