题目内容
在等差数列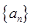 中,
中,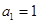 ,前
,前 项和
项和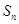 满足条件
满足条件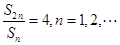 ,
,
(1)求数列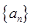 的通项公式和
的通项公式和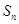 ;(2)记
;(2)记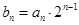 ,求数列
,求数列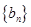 的前
的前 项和
项和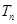 .
.
(1)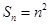 ,(2)
,(2)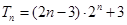 .
.
解析试题分析:(1)求等差数列问题,一般利用待定系数法求解. 设等差数列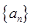 的公差为
的公差为 ,由
,由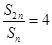 得:
得: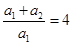 ,所以
,所以 ,且
,且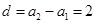 ,所以
,所以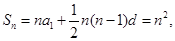 (2)由
(2)由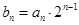 ,得
,得 这是等差乘等比型,因此利用错位相减法求和.
这是等差乘等比型,因此利用错位相减法求和. 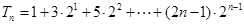 ,
,
两式相减得:
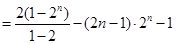 ,所以
,所以 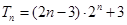 .
.
解:(1)设等差数列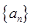 的公差为
的公差为 ,由
,由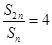
得: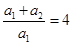 ,所以
,所以 ,且
,且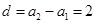 , 3分
, 3分
所以 5分
5分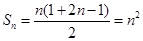 7分
7分
(2)由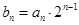 ,得
,得 8分
8分
所以 , ① 9分
, ① 9分  , ② 11分
, ② 11分
① ②得 13分
13分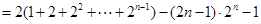
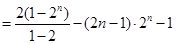 15分
15分
所以 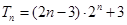 16分
16分
考点:等差数列,错位相减法求和

练习册系列答案
相关题目
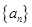 的前
的前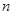 项和
项和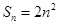 ,
,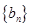 为等比数列,且
为等比数列,且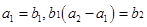 .
.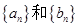 的通项公式;(2)设
的通项公式;(2)设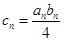 ,求数列
,求数列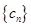 前
前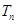 .
.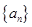 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项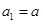 ,
,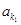 、
、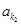 、…、
、…、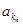 恰为等比数列,且
恰为等比数列,且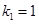 ,
,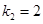 ,
,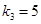 .
. (用
(用 表示);
表示); 的前
的前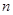 项和为
项和为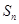 ,求
,求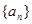 是一个等差数列且
是一个等差数列且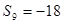 ,
,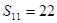 ,
, 项和
项和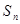 的最小值.
的最小值.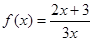 , 数列
, 数列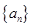 满足
满足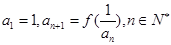 .
.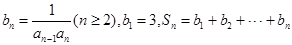 ,若
,若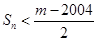 对一切
对一切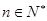 成立,求最小正整数m.
成立,求最小正整数m.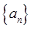 的前
的前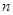 项和为
项和为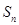 ,
,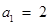 ,
,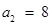 ,
,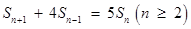 ,
,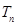 是数列
是数列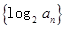 的前
的前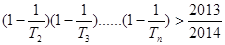 的最大正整数
的最大正整数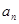 }的前n项和
}的前n项和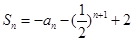 (n为正整数)。
(n为正整数)。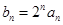 ,求证数列{
,求证数列{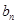 }是等差数列,并求数列{
}是等差数列,并求数列{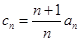 ,
,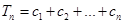 ,求
,求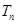 并证明:
并证明: