题目内容
【题目】某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心. 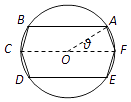
(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);
(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.
【答案】
(1)解:作AH⊥CF于H,
则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,
则六边形的面积为f (θ)=2× ![]() (AB+CF)×AH=(2cosθ+2)sinθ
(AB+CF)×AH=(2cosθ+2)sinθ
=2(cosθ+1)sinθ,θ∈(0, ![]() )
)
(2)解:f′(θ)=2[﹣sinθsinθ+(cosθ+1)cosθ]
=2(2cos2θ+cosθ﹣1)=2(2cosθ﹣1)(cosθ+1).
令 f′(θ)=0,因为θ∈(0, ![]() ),
),
所以cosθ= ![]() ,即θ=
,即θ= ![]() ,
,
当θ∈(0, ![]() )时,f′(θ)>0,所以f (θ)在(0,
)时,f′(θ)>0,所以f (θ)在(0, ![]() )上单调递增;
)上单调递增;
当θ∈( ![]() ,
, ![]() )时,f′(θ)<0,所以f (θ)在(
)时,f′(θ)<0,所以f (θ)在( ![]() ,
, ![]() )上单调递减,
)上单调递减,
所以当θ= ![]() 时,f (θ)取最大值f (
时,f (θ)取最大值f ( ![]() )=2(cos
)=2(cos ![]() +1)sin
+1)sin ![]() =
= ![]() .
.
答:当θ= ![]() 时,可使得六边形区域面积达到最大,最大面积为
时,可使得六边形区域面积达到最大,最大面积为 ![]() 平方百米
平方百米
【解析】(1)作AH⊥CF于H,则六边形的面积为f (θ)=2(cosθ+1)sinθ,θ∈(0, ![]() ).(2)求导,分析函数的单调性,进而可得θ=
).(2)求导,分析函数的单调性,进而可得θ= ![]() 时,f (θ)取最大值.
时,f (θ)取最大值.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
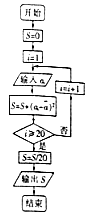
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值.