题目内容
【题目】已知等差数列![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 满足关系式
满足关系式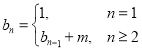 ,求证:数列
,求证:数列![]() 的通项公式为
的通项公式为![]() ;
;
(3)设(2)中的数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,
,对任意的正整数n,![]() 恒成立,求实数p的取值范围.
恒成立,求实数p的取值范围.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由等差数列由通项公式,得到首项与公差的方程组,得出首项与公差的值,得到通项公式;
(2)已知数列的递推公式,由叠加法,得到数列的通项公式;
(3)将数列求和得到前n项和后,将条件变形后,得到关于参数p的关系式,这是一个恒成立问题,通过最值的研究,得到本题结论.
(1)设等差数列![]() 的公差为d,
的公差为d,
由已知,有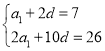 ,
,
解得![]()
所以![]() ,
,
即等差数列![]() 的通项公式为
的通项公式为![]() ,
,![]() .
.
(2)因为![]() ,
,
所以,当![]() 时,
时,![]() .
.
证法一(数学归纳法):
①当![]() 时,
时,![]() ,结论成立;
,结论成立;
②假设当![]() 时结论成立,即
时结论成立,即![]() ,
,
那么当![]() 时,
时,![]() ,
,
即![]() 时,结论也成立.
时,结论也成立.
由①,②得,当![]() 时,
时,![]() 成立.
成立.
证法二:当![]() 时,
时,![]() ,
,
所以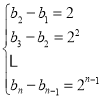
将这![]() 个式子相加,得
个式子相加,得![]() ,
,
即![]() .
.
当![]() 时,
时,![]() 也满足上式.
也满足上式.
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(3)由(2)![]() ,所以
,所以![]() ,
,
![]() 原不等式变为
原不等式变为![]() ,即
,即![]() ,
,
![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() 为任意的正整数,
为任意的正整数,
![]() .
.
![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目