Question

（2011•上海模拟）对于任意的实数k，如果关于x的方程f（x）=k最多有2个不同的实数解，则|f（x）|=m（m为实常数）的不同的实数解的个数最多为

4

．

Answer 1

分析：由题意可得，f（x）必定在某点a两侧单调性相反，它的也就是个“V”型，|f（x）|的图象有最多的相反单调区间，就是个“W”型，数形结合得出结论．

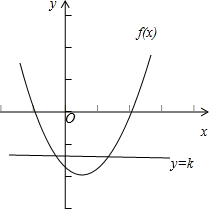
解答：解：由k的条件可以了解到，最多2解的条件下，f（x）必定在某点a两侧单调性相反，它的也就是个“V”型．这样当a点f（x）值为负，无穷点处值为正时，
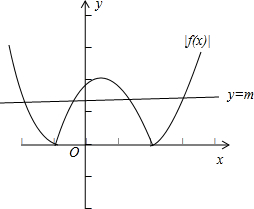
|f（x）|的图象有最多的相反单调区间，就是个“W”型，这时这个“W”图象与某条直线y=m的交点最多有4个．
如图所示：
故答案为 4．

点评：本题主要考查方程的根的存在性及个数判断，数形结合的思想确实很重要，属于中档题．