题目内容
设函数f(x) =x3-6x+5,x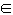 R.
R.
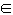 R.
R. (1)求函数f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有三个不同实根,求实数a的取值范围;
(3)已知当x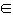 (1,+
(1,+ )时,f(x)≥k(x-1)恒成立,求实数k的取值范围.
)时,f(x)≥k(x-1)恒成立,求实数k的取值范围.
(2)若关于x的方程f(x)=a有三个不同实根,求实数a的取值范围;
(3)已知当x
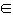 (1,+
(1,+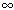 )时,f(x)≥k(x-1)恒成立,求实数k的取值范围.
)时,f(x)≥k(x-1)恒成立,求实数k的取值范围.解:(1)f '(x)=3x2-6,令f '(x)=0,解得x1=-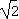 ,x2=
,x2=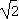 .
.
因为当x>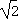 或x<-
或x<-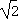 时,f '(x)>0;
时,f '(x)>0;
当-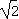 <x<
<x<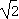 时,f '(x)<0.
时,f '(x)<0.
所以f(x)的单调递增区间为(-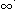 ,-
,-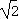 )和(
)和(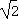 ,+
,+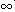 );单调减区间为(-
);单调减区间为(-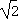 ,
,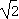 ).
).
当x=-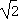 时,f(x)有极大值5+4
时,f(x)有极大值5+4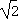 ;
;
当x=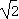 时,f(x)有极小值5-4
时,f(x)有极小值5-4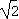 .
.
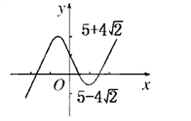
(2)由(1)的分析知y=f(x)的图象的大致形状及走向如图所示,
当5-4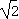 <a<5+4
<a<5+4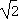 时,直线y=a与y=f(x)的图象有三个不同交点,
时,直线y=a与y=f(x)的图象有三个不同交点,
即方程f(x)=a有三个不同的解.
(3)f(x)≥k (x-1),即(x-1)(x2+x-5)≥k(x-1).
因为x>1,所以k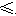 x2+x-5在(1,+
x2+x-5在(1,+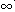 )上恒成立.
)上恒成立.
令g(x)=x2+x-5,此函数在(1,+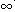 )上是增函数.
)上是增函数.
所以g(x)>g(1)=-3.
所以k的取值范围是k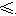 -3.
-3.
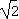 ,x2=
,x2=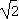 .
.因为当x>
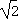 或x<-
或x<-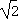 时,f '(x)>0;
时,f '(x)>0;当-
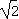 <x<
<x<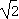 时,f '(x)<0.
时,f '(x)<0.所以f(x)的单调递增区间为(-
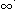 ,-
,-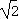 )和(
)和(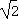 ,+
,+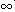 );单调减区间为(-
);单调减区间为(- ,
,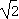 ).
).当x=-
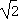 时,f(x)有极大值5+4
时,f(x)有极大值5+4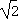 ;
;当x=
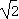 时,f(x)有极小值5-4
时,f(x)有极小值5-4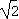 .
.(2)由(1)的分析知y=f(x)的图象的大致形状及走向如图所示,
当5-4
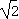 <a<5+4
<a<5+4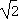 时,直线y=a与y=f(x)的图象有三个不同交点,
时,直线y=a与y=f(x)的图象有三个不同交点,即方程f(x)=a有三个不同的解.
(3)f(x)≥k (x-1),即(x-1)(x2+x-5)≥k(x-1).
因为x>1,所以k
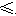 x2+x-5在(1,+
x2+x-5在(1,+ )上恒成立.
)上恒成立.令g(x)=x2+x-5,此函数在(1,+
 )上是增函数.
)上是增函数.所以g(x)>g(1)=-3.
所以k的取值范围是k
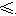 -3.
-3.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
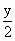 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.