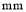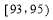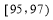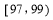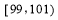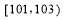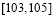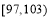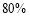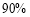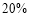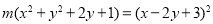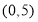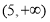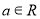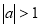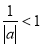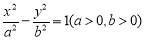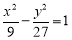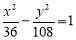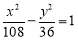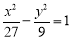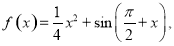题目内容
已知双曲线
－
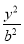＝1(a>0，b>0)的左、右焦点分别为F1(－c,0)、F2(c,0)．若双曲线上存在点P，使
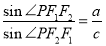，则该双曲线的离心率的取值范围是________．
【解析】
试题分析：根据正弦定理与题中等式，算出
=e（e是椭圆的离心率）．作出椭圆的左准线l，作PQ⊥l于Q，根据椭圆的第二定义得
＝e，所以|PQ|=|PF2|=
．设P（x，y），将|PF1|、|PF2|表示为关于a、c、e、x的式子，利用|PF2|+|PF1|=2a解出x=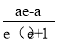
．最后根据椭圆上点的横坐标满足-a≤x≤a，建立关于e的不等式并解之，即可得到该椭圆离心率的取值范围．
考点：(1)正弦定理；（2）椭圆的定义；（3）椭圆的几何性质.
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
