题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(Ⅰ)求证数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅲ)对任意 ![]() ,试比较
,试比较 ![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)由![]() 得
得![]() ,二式相减得:
,二式相减得:![]() ,
,
∴ 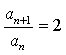 ,∴数列
,∴数列![]() 是公比为2的等比数列, ………………………3分
是公比为2的等比数列, ………………………3分
又∵![]() . ………………………5分
. ………………………5分
(Ⅱ) ∵![]() ,
,
∴![]() ①
①
![]() ,② …………7分
,② …………7分
①-②得![]()
![]() ,
,
∴![]() . ………………………9分
. ………………………9分
(Ⅲ)∵![]() ,
,
∴![]() , ………………………11分
, ………………………11分
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() . …………………………13分
. …………………………13分
综上,当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() . …………………………14分
. …………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前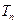 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 与
与 两项之间插入
两项之间插入 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且满足
,且满足
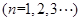 .
. 为等比数列;
为等比数列; ;
; 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列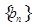 的前
的前 .
. 
 的前
的前 项和为
项和为 ,且
,且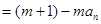 对于
对于 为常数,且
为常数,且
 ,数列
,数列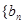

 ,
,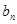
 )(
)( ,
, ,求证:数列
,求证:数列

