题目内容
设数列 的前
的前 项和为
项和为 ,且满足
,且满足
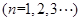 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)求通项公式 ;
;
(Ⅲ)若数列 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列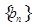 的前
的前 项和为
项和为 .
.
【答案】
(Ⅰ)见解析 (Ⅱ) . (Ⅲ)
. (Ⅲ) .
.
【解析】(I)根据 ,可得
,可得 ,
,
从而可证明: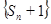 为等比数列.
为等比数列.
(II)在(I)的基础上先求出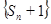 的通项公式,然后再根据Sn求出an.
的通项公式,然后再根据Sn求出an.
(III)先求出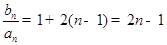 ,
,
再根据an的通项公式求出bn,由于 ,所以易采用错位相减的方法求和
,所以易采用错位相减的方法求和
证明:(Ⅰ)因为  ,所以
,所以 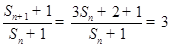 . 又
. 又 ,
,
所以 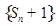 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(Ⅱ)由(Ⅰ)可得 .当
.当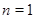 时,
时,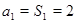 .
.
当 时,
时,

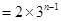 .
.
故 .
.
(Ⅲ)因为 数列 是首项为1,公差为2的等差数列,所以
是首项为1,公差为2的等差数列,所以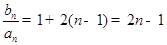 .所以
.所以  .
.
所以  .
.
所以 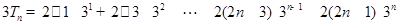 .
.
所以 
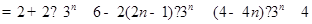 .
.
所以  .
.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前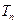 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 与
与 两项之间插入
两项之间插入 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 .
.
 的前
的前 项和为
项和为 ,且
,且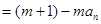 对于
对于 为常数,且
为常数,且
 ,数列
,数列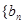

 ,
,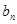
 )(
)( ,
, ,求证:数列
,求证:数列

