题目内容
设数列 的前
的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)在数列 的每两项之间按照如下规则插入一些数后,构成新数列:
的每两项之间按照如下规则插入一些数后,构成新数列: 与
与 两项之间插入
两项之间插入 个数,使这
个数,使这 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
【答案】
(1)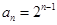 ;(2)
;(2)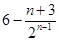 .
.
【解析】
试题分析:(1)一般已知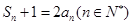 ,则
,则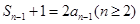 两式相减求出
两式相减求出 ;(2)利用错位相减法求和.
;(2)利用错位相减法求和.
试题解析:(1)当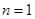 时,
时,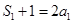 ,∴
,∴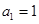 . (2分)
. (2分)
当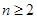 时,又
时,又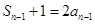 ,∴
,∴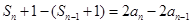 ,即
,即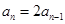 ,
,
∴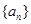 是以1为首项,2为公比的等比数列,故
是以1为首项,2为公比的等比数列,故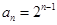 .
(6分)
.
(6分)
(2)由(1)得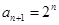 ,则
,则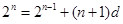 ,∴
,∴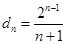 ,
,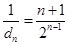 , (8分)
, (8分)
∴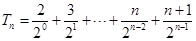 ,
,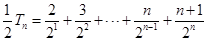 ,
(10分)
,
(10分)
两式相减得: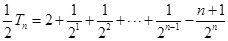 ,
,
∴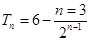 .
(13分)
.
(13分)
考点:数列的通项公式,数列求和.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前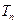 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足
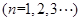 .
. 为等比数列;
为等比数列; ;
; 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列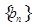 的前
的前 .
. 
 的前
的前 项和为
项和为 ,且
,且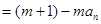 对于
对于 为常数,且
为常数,且
 ,数列
,数列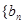

 ,
,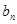
 )(
)( ,
, ,求证:数列
,求证:数列

